Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Synthetic Division

Show all necessary work. The test is worth 106 points.
For problems 1-6, use f(x) = 8x – 13 and g(x) = x² – 5. (5 points each)
1. (f + g) (-2) = __________ 4. (f – g) (3) = __________
2. (fg) (2) = __________ 5. (f ◦ g) (1) = __________
3. (g ◦ f) (1) = __________ 6. f^-1(x) = __________

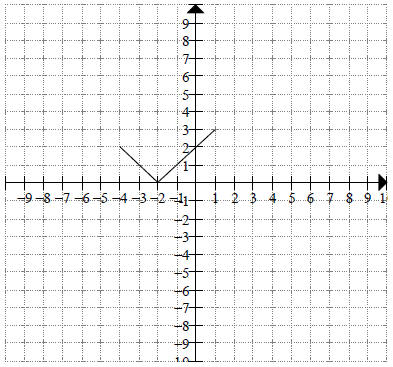
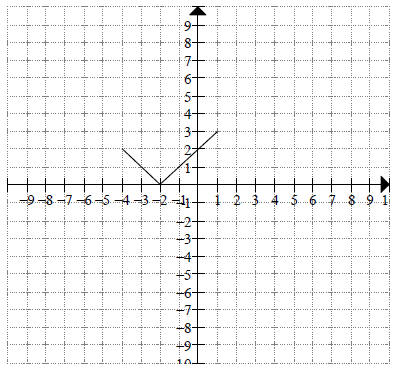
(4 points each) For problems 7 and 8, given the graph of y = f(x), sketch the graph of:

7. y = f(x + 2) + 3

8. y = -2 f(x)

9. Let f(x) = 2x² + 8x – 5.
a) (5 points) Find the vertex.

b) (5 points) Write f(x) in shifted form.

10. Let f(x) = 3x³ – 7x² – 22x + 8.
a) (5 points) Use the Rational Zero Theorem to list all possible rational
zeroes of f(x).

b) (5 points) Find all of the zeroes of f(x). Use synthetic division if necessary.

c) (4 points) Write f(x) in factored form.

11. (8 points) Let f(x) = x³ + 5x² – 3x – 27. Given that x = -3 is a zero of this
polynomial, use synthetic division and the quadratic formula to find the other
two zeroes.

Multiple Choice (4 points each) Choose the best response.

12. Let f(x) be a one-to-one function with domain 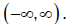What is ?
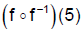a) 5 b) -5 c) − 1/5 d) cannot be determined

13. Let f(x) = 2x² – 11x – 40. Find the axis of symmetry.

14. Let f(x) = 2x² – 11x – 40. Find the x-intercepts.
a) (-2.5, 0) and (8, 0) c) (2.5, 0) and (-8, 0)
b) (2.5, 0) and (8, 0) d) (-2.5, 0) and (8, 0)

15. When a polynomial f(x) is divided by x – 4 using synthetic division, the last line
of the synthetic division is:

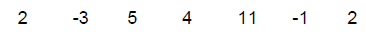
What is the quotient?
a) 2x⁶– 3x⁵ + 5x⁴ + 4x³ + 11x² – x + 2
b) 2x⁵ – 3x⁴ + 5x³ + 4x² + 11x – 1
c) cannot be determined because we don't know f(x)

16. When a polynomial f(x) is divided by x + 3 using synthetic division, the last line
of the synthetic division is:

What is f(-3)?
a) cannot be determined b) 8 c) 7
because we don't know f(x)

Use f(x) = -3 (x + 2)⁵ (x – 1)⁶(x – 5)² (2x + 3)² for problems 17-20.

17. The degree of this polynomial is:
a) 2 b) 5 c) 6 d) 15

18. The leading coefficient of this polynomial is:
a) -3 b) 6 c) -12 d) -6

19. When graphing this polynomial:
a) the left "arm" will go up and the right "arm" will go down
b) the left "arm" will go down and the right "arm" will go up
c) both "arms" will go up
d) both "arms" will go down

20. The graph of this polynomial will:
a) "bounce" at one zero and "cross" at three zeroes
b) "bounce" at three zeroes and "cross" at one zero
c) "bounce" at all four zeroes
d) "cross" at all four zeroes

Home