22A Summer II 2009 Final Review Sheet
Be able to state (with words and symbols) the
definition
of the following terms
• Subspace
• linear combination of the vectors
.
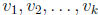• A set of vectors span a vector space
• Basis, dimension
• The nullspace, column space, row space for an m × n matrix A
• The rank and nullity of a matrix A
• eigenvalues for a matrix A
• eigenvectors associated to an eigenvalue λ for a matrix A
• The associated eigenspace for an eigenvalue λ for a matrix A
• characteristic polynomial of a matrix A
• symmetric, diagonal, upper-triangular, lower-triangular, and orthogonal
matrices
• diagonalizability of a matrix A and orthogonally diagonalizabity of A
• Linear transformation from Rm to Rn
• The standard matrix for a linear transformation
• range of a linear transformation
• orthogonal vectors in Rn, an orthonormal set of vectors in Rn and
orthonormal basis in Rn
• a 1-1 function
• a onto function
• The coordinate vector with respect to a given ordered basis
• The transition matrix ( or change of coordinate matrix) from one ordered
basis to another ordered basis
Know the statement of and how to use
• Rank Nullity Theorem
• Algebraic properties of matrix operations
• Algebraic properties of inverse matrices
• Algebraic properties of determinants
• Algebraic properties of vector operations
• Algebraic properties of linear transformations
• Algebraic properties of abstract vector space operations
• Algebraic properites of eigenvectors
• The various equivalences for nonsingularity for a matrix A (see pg. 204
in the book)
• The algebraic properties of coordinate vectors and transition matrices
Be able to
• Prove or disprove a statement about abstract operations
• Be able to determine if a subset of a vector space V is a subspace of V
• Be able to determine if a set of vectors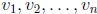 
in a vector space
V
– spans V
– is linearly independent
– is a basis for V
• Solve for the general solution for a linear system
• Recognize row echelon forms and reduced row echelon forms (RREF)
• Use elementary row operations to get a RREF
• Understand what a REF tells us about the solutions to a linear system
• Be able to compute the general solution for a homogeneous system
• Be able to compute determinants
• Be able to determine whether or not a given matrix is invertible and if
so find its inverse
• Be able to find a basis for the null space of A
• Be able to find a basis for the column space and row space of A
• Be able to compute the rank and nullity of a matrix A
• Be able to find a basis for W = span{}
• Be able to use Gram-Schmidt to orthonormalize a basis
• Be able to verify if a set of vectors is orthonormal and know examples
of orthonormal basis
• Be able to compute eigenvalues of a matrix A
• Be able to find associated eigenvectors for a given eigenvalue
• Be able to find a basis for the eigenspace Eλ for a matrix A
• Be able to determine if a matrix A is diagonalizable and if so be able
to find a matrix P so that P-1AP is diagonal
• For a symmetric matrix A be able to find orthogonal matrix P so that
P-1AP is diagonal
• Be able to verify if matrix A is orthogonal
• Be able to determine if a vector is a linear combination of other vectors
• Be able to determine if another vector is in the range of a linear
transformation
• Be able to find a basis for the range of a linear transformation
• Be able to find the standard matrix of a linear transformation
• Be able to recognize whether or not a given function is linear or not
linear
• Determine if a linear transformation is 1-1 and/or onto.
• Understand the various equivalences for nonsingularity for a matrix A
(see pg. 204 in the book)
• Understand the various algebraic properties of the various operations
in linear algebra and how to give basic algebraic proofs using these
properties
• Understand how to setup linear system in order to answer various linear
algebra questions
• Be able to find the coordinate vector with respect to a given ordered
basis
• Be able to find the transition matrix from one ordered basis to another
ordered basis
• Be able to find the vector in a vector space that a given coordinate
vector with respect to an ordered basis represents
Be sure to review
• All lecture notes
• All WebWork assignments
• All reading assignments (except Sec. 1.8)
• All suggested problems
DO NOT
• Wait until the night before to study
• Merely memorize problems. Try to understand the methods and concepts
involved.
• Only Study the old Final and expect to succeed.
