Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

New Functions from Old Functions

Important: Even though we are starting with 1.3, you should read all of Chapter 1. This
should be mostly review of topics you've seen in previous courses.

I. Some Function Basics

Definitions (from 1.1)

A function f is a rule that assigns each element x in a set A exactly one element, called
f(x), in a set B.

The set A is called the domain. The set of all f(x) is called the range (a subset of B).

Representations of Functions (from 1.1)

There are four possible ways to represent a function:

1. Verbally: by a description in words

2. Numerically: by a table of values

3. Visually: by a graph, or arrow diagram, or "machine"

4. Algebraically: by an explicit formula

The Vertical Line Test (from 1.1)

A curve in the xy-plane is the graph of a function of x if and only if no vertical line intersects
the curve more than once. (A graphical way to test if you have a function.)

II. Transformations of Functions

Vertical and Horizontal Shifts (Translations)

Suppose c > 0. To obtain the graph of
y = f(x) + c, shift the graph of y = f(x) a distance c units upward
y = f(x) - c, shift the graph of y = f(x) a distance c units downward
y = f(x - c), shift the graph of y = f(x) a distance c units to the right
y = f(x + c), shift the graph of y = f(x) a distance c units to the left

Example 1 Given f(x) = x², graph f(x - 2), f(x) - 2, f(x + 2), and f(x) + 2.

Example 2 (from Stewart) Problem 4, page 46, parts (a) and (b).

Vertical and Horizontal Stretching and Reflecting

Suppose c > 1. To obtain the graph of
y = cf(x), stretch the graph of y = f(x) vertically by a factor of c
y = (1/c)f(x), compress the graph of y = f(x) vertically by a factor of c
y = f(cx), compress the graph of y = f(x) horizontally by a factor of c
y = f(x/c), stretch the graph of y = f(x) horizontally by a factor of c
y = -f(x), reflect the graph of y = f(x) about the x-axis
y = f(-x), reflect the graph of y = f(x) about the y-axis

Example 3 Given f(x) = sin(2π x), graph f(2x), f(x/2), 2f(x), -f(x), and f(-x).

Example 4 (from Stewart) Problem 4, page 46, parts (c) and (d).

III. Combinations of Functions

Algebra of Functions

Let f and g be functions with domains A and B. Then the functions f + g, f - g, fg, and
f/g are defined as follows:

Example 5 (from Stewart) Example 6, page 43. If 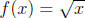and 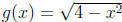, find
the functions f + g, f - g, fg, and f/g. Also, what is the new domain in each case?

IV. Composition of Functions

Definition

Given two functions f and g, the composite function f o g (also called the composition
of f and g) is defined by

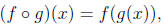
where the domain of f o g is the set of all x in the domain of g such that g(x) is in the
domain of f.

Remember: In general,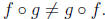

Example 6 Let f(x) = 1/x and let g(x) = x - 2, find f o g and g o f. (Notice that
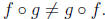) What is the domain in each case?

Example 7 Let f(x) = x² and let g(x) = x - 2. What type of transformation of the graph
of f does f o g represent?

Home