Negative Exponents and Scientific Notation
Overview
• Section 5.2 in the textbook
– Expressions with negative exponents
– Simplifying more complex exponential
expressions
–Writing numbers in scientific notation
– Scientific notation to standard form
Expressions with Negative
Exponents
• Consider x2 / x6
x-4 by the quotient rule
x·x / x·x·x·x·x·x
1 / x4
• Usually, we do NOT leave an expression
with a negative exponent
• Flipping an exponent AND its base from
the numerator into the denominator (or
vice versa) reverses the sign of the
exponent
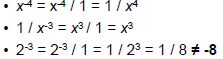
– The sign of the exponent DOES NOT affect
the sign of the base!
–Whenever using the quotient rule, the initial
result goes into the numerator
Expressions with Negative
Exponents (Example)
Ex 1: Simplify – leave NO negative exponents:
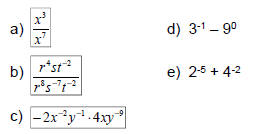
Simplifying More Complex
Exponential Expressions
Reviewing the Exponent Rules
• Product Rule: 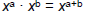
• Power Rule: 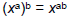
– Power of a Product: 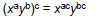
– Power of a Quotient: 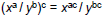
• Quotient Rule: 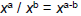
Simplifying More Complex
Exponential Expressions
• When solving more complicated
expressions:
– Simplify inside of the parentheses using the
product and quotient rules if possible
– Apply the power (if one exists)
• Use the power rule with the exponents
• Evaluate the bases as with normal numbers
– If necessary, write the final answer with
positive exponents
Simplifying More Complex
Exponential Expressions (Example)
Ex 2: Simplify – leave NO negative
exponents:
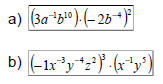
Ex 3: Simplify – leave NO negative
exponents:
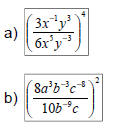
Ex 4: Simplify – leave NO negative
exponents:
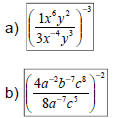
Writing Numbers in Scientific
Notation
• Scientific Notation: any number in the
form of a x 10b where -10 < a < 10, a ≠ 0
and b is an integer
– Used to write extreme numbers (large or
small) in a compact format
• To write a number in scientific notation:
– One non-zero number to the left of the
decimal point – the rest to the right
– Determine where to place the decimal point:
• Count how many places the decimal point is
moved
• If the original number (without the sign) is greater
than 1, b (the exponent) is positive
• If the original number (without the sign) is less than
1, b is negative
Writing Numbers in Scientific
Notation (Example)
Ex 5: Write each in scientific notation:
a) -238.41
b) 0.00584
c) 0.018
More with Scientific Notation
Scientific Notation to Standard
Form
• Standard Notation: writing a number in
scientific notation without the power of ten
– Take the decimal and move it:
• To the right if b (the exponent) is positive
• To the left if b (the exponent) is negative
• Fill in empty spots with zeros
Scientific Notation to Standard
Form (Example)
Ex 6: Write in standard notation:
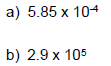
Multiplying or Dividing in Scientific
Notation
• Multiply or divide the numbers as normal
• Use the Product or Quotient Rules to
simplify the power of tens
• Write the final answer in scientific notation
Multiplying or Dividing in
Scientific Notation (Example)
Ex 7: Simplify and write as a single number
in scientific notation:
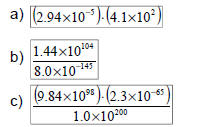
Summary
• After studying these slides, you should know
how to do the following:
– Simplify expressions containing negative exponents
– Apply the exponent rules to simplify more complex
exponential expressions
– Writing numbers in scientific notation
– Converting scientific notation to standard form
– Multiply or divide using scientific notation
• Additional Practice
– See the list of suggested problems for 5.2
• Next lesson
– Introduction to Polynomials (Section 5.3)


