NEW MATH PLACEMENT TEST REVIEW
101. Simplify:
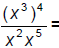
102. Simplify:
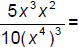
103. Simplify:
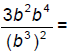
104. Simplify: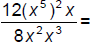
105. Simplify:
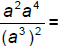
106. Simplify:
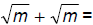
107. Simplify:
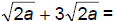
108. Simplify:
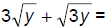
109. Simplify:
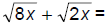
110. Simplify:
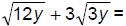
111. Simplify:
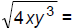
112. Simplify:
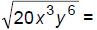
113. Simplify:
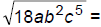
114. Simplify:
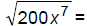
115. If D = RT, then T =
116. If P = 2A + 2B, then A =
117. If 3m + 2n = k, then m =
118. If I = PRT, then P =
119. If 2x – 3y = z, then y =
120. If x – 4y = 12, then the y-intercept of the graph of this equation is:
121. If 3x + y = 12, then the x-intercept of the graph of this equation is:
122. If 3x – 2y = 24, then the y-intercept of the graph of this equation is:
123. If 2x + y = 7, then the x-intercept of the graph of this equation is:
124. If 2x + 3y = 10, then the y-intercept of the graph of this equation is:
125. Reduce:
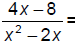
126. Reduce: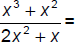
127. Reduce: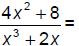
128. Reduce: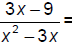
129. Reduce: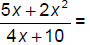
130. Factor: 2x2 – 8 =
131. Factor: 3x2 – 27 =
132. Factor: 32 – 2x2 =
133. Factor: 50 – 2x2 =
134. Factor: kx2 – 9k =
135. Add: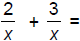
136. Add: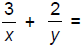
137. Subtract: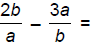
138. Multiply: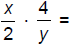
139. Multiply:
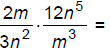
140. Divide: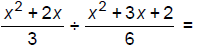
141. One of the roots of x2 – x – 1 = 0 is:
142. One of the roots of x2 –2 x – 1 = 0 is:
143. One of the roots of x2 + x – 4 = 0 is:
144. One of the roots of 2x2 –3 x – 2 = 0 is:
145. One of the roots of 3x2 + x – 1 = 0 is:
146. The graph of y = 3 is a: (a) line (b) horizontal line (c) vertical line
(d) parabola (e) circle (f) ellipse (g) hyperbola (h) none of the above
147. The graph of 2x + y = 6 is a: (a) line (b) horizontal line (c) vertical
line (d) parabola (e) circle (f) ellipse (g) hyperbola (h) none of the
above
148. The graph of 2x2 + y = 6 is a: (a) line (b) horizontal line (c) vertical
line (d) parabola (e) circle (f) ellipse (g) hyperbola (h) none of the
above
149. The graph of 2x2 + y2 = 6 is a: (a) line (b) horizontal line (c) vertical
line (d) parabola (e) circle (f) ellipse (g) hyperbola (h) none of the
above
150. The graph of 3x + y2 = 0 is a: (a) line (b) horizontal line (c) vertical
line (d) parabola (e) circle (f) ellipse (g) hyperbola (h) none of the
above
151. The graph of x2 + y2 = 9 is a: (a) line (b) horizontal line (c) vertical
line (d) parabola (e) circle (f) ellipse (g) hyperbola (h) none of the
above
152. The graph of 4x2 – 9y2 = 36 is a: (a) line (b) horizontal line (c)
vertical line (d) parabola (e) circle (f) ellipse (g) hyperbola (h) none of
the above
153. The graph of
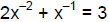is a: (a) line (b) horizontal line (c) vertical
line (d) parabola (e) circle (f) ellipse (g) hyperbola (h) none of the
above
154. The graph of x2 – y = 0 is a: (a) line (b) horizontal line (c) vertical
line
(d) parabola (e) circle (f) ellipse (g) hyperbola (h) none of the above
155. Simplify: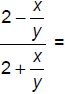
156. Simplify: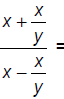
157. Simplify: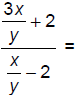
158. Simplify: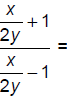
159. Simplify: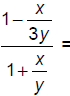
160. If 3a + 2b – 4ab = 8, then b =
161. If 2xy + 3y – 4x = 1, then x =
162. If 4b – 2a – ab = 11, then a =
163. If 3x – 2xy = 4y + 8, then y =
164. If 5b + 2c = 3bc – 6, then c =
165. Solve for x: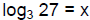
166. Solve for x:
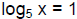
167. Solve for x:
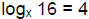
168. Solve for x: log x = 0
169. Solve for x:
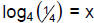
170. Solve for x: | x – 3 | > 2
171. Solve for x: | 3x + 2 | < 1
172. Solve for x: | 3 – x | > 5
173. Solve for x: | 4 + 2x | > 6
174. Solve for x: | 2x – 5 | ≤3
175. Find f (–1) if f (x) = 2x + 1
176. Find f (–3) if f (x) = 3x2 – x
177. Find f (2) if f (x) = 4x2 + 7
178. Find f (–2) if f (x) = –x2 + 4x + 1
179. Find f (3) if f (x) = x2 – x – 3
180. The graphs of 3x – y = 2 and y = 2x – 1 intersect at what point?
181. The graphs of x – 2y = 3 and y = 2x – 4 intersect at what point?
182. The graphs of x = 2 and 2y = x – 1 intersect at what point?
183. The graphs of 3x + y = 2 and y = 2x – 1 intersect at what point?
184. The graphs of 3x + y = 1 and y = – 2 intersect at what point?
185. Which equation best describes this graph:
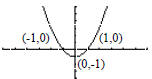
186. Which equation best describes this graph:
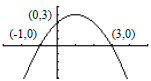
187. Which equation best describes this graph:
188. Which equation best describes this graph:
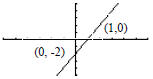
189. Which equation best describes this graph:
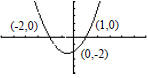
190. A square lot has an area of 200 square feet. If w represents the length
of a side, then an equation that can be used to determine the value of w is:
191. A rectangular playground with area 480 square feet has a length that is
two feet more than twice of its width. If w represents the width of the field,
then an equation that can be used to determine the value of w is:
192. A triangle with area 175 square feet has a base that is three feet less
than twice its height. If h represents the height of this triangle, then an
equation that can be used to determine the value of h is:
193. A rectangular field with area 266 square feet has a width that is five feet
less than its length. If w represents the width of the field, then an equation
that can be used to determine the value of w is:
194. A rectangular pool with perimeter of 112 meters has a length that is four
meters more than its width. If w represents the width of the pool, then an
equation that can be used to determine the value of w is:
195. If
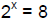, then the exact value of x is:
196. If
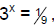then the exact value of x is:
197. If 8x= 1, then the exact value of x is:
198. If 5x= 7, then the exact value of x is:
199. If 3x= 4, then the exact value of x is:
200. If f(x) = 3x –1 and g(x) = x2 + 3, then f(g(x)) =
