Math 2312 TEST 2
_________________________________________________________________
READ ME FIRST: Show all essential work very neatly.
Use correct notation
when presenting your computations and arguments. Write using complete
sentences. Be careful. Remember this: "=" denotes "equals" , "⇒"
denotes "implies" , and "⇔" denotes "is equivalent to". Since the answer
really consists of all the magic transformations, do not "box" your final
results. Communicate. Show me all the magic on the page.
_________________________________________________________________
1. (10 pts.) (a) Sketch the region in the first quadrant enclosed by the
curves y = cos-1(x), x = 0, and y = 0. (b) Using the method of disks or
washers, write a single definite integral whose numerical value is the
volume of the solid obtained when the region is revolved around the x-axis.
Do not evaluate the integral. (c) Using the method of cylindrical shells,
write down a definite integralto compute the same volume as in part (b).
Do not evaluate the integral.
 |
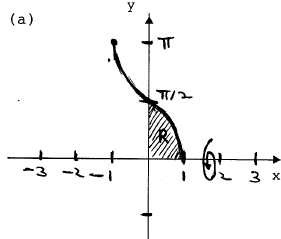(b) For -1 ≤ x ≤ 1 and 0 ≤ y ≤ π y cos-1(x) ⇔ x cos(y). 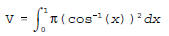 (c)  |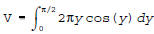
_________________________________________________________________
2. (10 pts.) (a) Write down, but do not attempt to
evaluate the definite
integral that gives the arc length along the curve defined by the equation
y = (1/2)x2 from x = -(3)1/2 to x = (3)1/2.
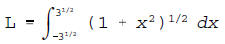
(b) Suppose a spring has a natural length of 1 foot, and a force of 10
pounds is needed to compress the spring to a length of 8 inches. Write
down the definite integral that gives the work done in stretching this
spring from its natural length to a total length of 15 inches but do not
attempt to evaluate the integral.
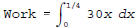since (1/3)k = 10 implies k = 30 using the
standard Work
Hooke's model.
_________________________________________________________________
3. ( 10 pts.) Consider the definite integral below. (a)
Write down the
sum,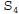 
, used to approximate the value of the integral below if Simpson's
Rule is used with n = 4. Do not attempt to evaluate the sum. Be very
careful. (b) Write down the sum,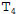 
, used to approximate the value of the
integral below if Trapezoid Rule is used with n = 4. Do not attempt to
evaluate the sum. Be very careful.
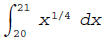
Plainly,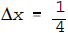 
, and
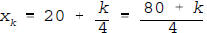, for k = 0,1,2,3,4
are the points of the regular partition we need.
(a)
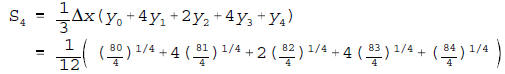
(b)
_________________________________________________________________
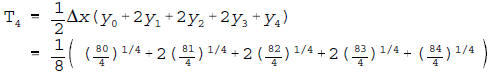
4. (10 pts.) (a) Using literal constants A, B, C, etc., write the form of
the partial fraction decomposition for the proper fraction below. Do not
attempt to obtain the actual numerical values of the constants A, B, C,
etc.
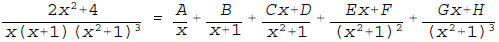
(b) If one were to integrate the rational function in part
(a), one
probably would encounter the integral below. Reveal, in detail, how to
evaluate this integral.
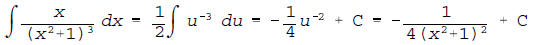
by using the obvious substitution u = x2 + 1. If you are
feeling feisty,
you can also handle this with a trigonometric substitution.
_________________________________________________________________
5. (10 pts.) (a) In making the substitution u = tan(x/2),
show all the
details in obtaining sin(x) and cos(x) in terms of u by correctly
completing the equations below. [Hint: It helps to draw a right triangle
to represent the equation u = tan(x/2).] (b) Show how to obtain the
differential dx in terms of du by solving for x in the equation u =
tan(x/2) and differentiating. (c) Using a sentence or two, explain what
this substitution does to integrals of rational functions of sine and
cosine.
| (a) (4 pts.) sin(x/2) = u/(u2 + 1)1/2 cos(x/2) = 1/(u2 + 1)1/2 sin(x) = sin(2(x/2)) = 2u/(u2 + 1) cos(x) = cos(2(x/2)) = ( 1 - u2 )/(u2 + 1) (b) (4 pts.) u = tan(x/2) implies x = 2tan-1(u). So dx = (2/(u2 + 1))du. |
|
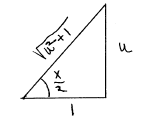
(c) (2 pt.) This substitution transforms integrals of rational functions
of sine and cosine into integrals of rational functions of u.
_________________________________________________________________
6. (10 pts.) Here are five trivial trigonometric integrals
to evaluate.
[2 pts./part]
_________________________________________________________________
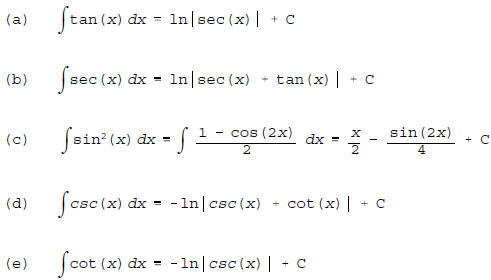
7. (40 pts.) Evaluate each of the following
antiderivatives or definite
integrals. Give exact values for definite integrals.
[5 pts./part]
(a)
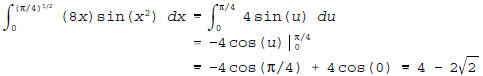
using the u-substitution u = x2.
(b)
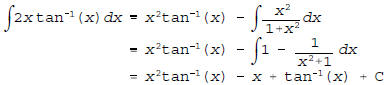
using parts with u = tan-1(x) and dv = 2x dx, followed by
a long
division.
(c)
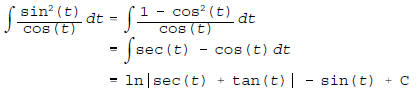
(d)
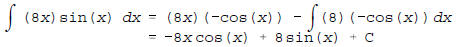
using integration by parts with u = 8x and dv = sin(x)dx.
(e)
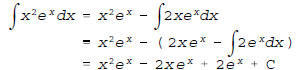
by integrating by parts twice. Keep picking on the
exponential
varmint as your recognized derivative.
(f)
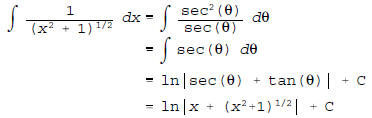
using the trigonometric substitution x = tan(θ).
(g)
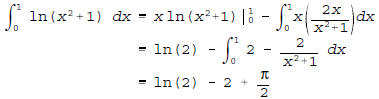
using integration by parts with u = ln(x2 + 1) and dv =
1dx followed
by long division.
(h)
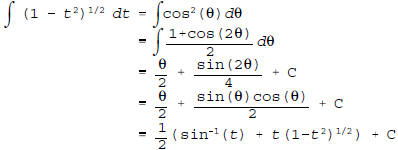
using the obvious trigonometric substitution t = sin(θ).
Of course
you could also try integration by parts, but htat route is a little
thornier.
_________________________________________________________________
Silly 10 Point Bonus: The magnitude of error in using
Simpson's Rule to
approximate the definite integral of f(x) on an interval [a,b] with n
subintervals may be estimated using
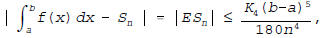
provided the fourth derivative of f,
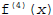, is
continuous on [a,b], and
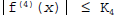for each x in [a,b]. If Simpson's rule is used to
approximate the definite integral giving the exact value of ln(2), reveal
how to determine how big must n be to ensure you have 2 decimal place
accuracy. [Say where your work is for there isn't room here. Remember n
must be even.]
