Addition and Subtraction of polynomials
A monomial is a number, a variable, or a product of
numbers and variables. The following
examples are monomials. The degree of a monomial is the sum of the exponents of
the
variables.
 |
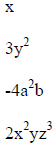Degree = 1  |
| Degree = 2 | |
| Degree = 3 | |
| Degree = 6 |
The degree of a nonzero constant is zero.
Ex: the degree of 7 is 0
Each of the addends of a variable expression is called a term. For example, the
following
variable expression:
4x – 3xy + 4z2
The terms are 4x, -3xy, and 4z2. Note that to determine the terms of an
expression, subtraction is
re-written as addition of the opposite.
A polynomial is a variable expression in which the terms are monomials.
| A polynomial of one term is a monomial | Example: |  |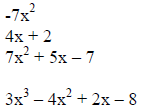
| A polynomial of two terms is a binomial | Example: | |
| A polynomial of three terms is a trinomial | Example: | |
| A polynomial of four or more terms is simply | ||
| called a polynomial | Example: |
The terms of a polynomial in one variable are usually
arranged so that the exponents of the
variable decrease from left to right. This
is called descending order.
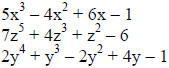
The degree of a polynomial is the degree of the term of largest degree.
The degree of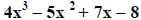 
is 3.
The degree of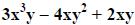 
is 4
Polynomials can be added, using either a horizontal or
vertical format, by combining like terms.
Simplify: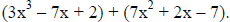 
Use a horizontal format.
 |
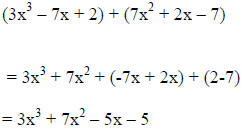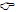 Use the
commutative and Associative properties of Addition to re-arrange and group like terms. |
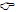| Then combine
like terms. |
Simplify: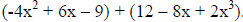 
Use a
vertical format.
 |
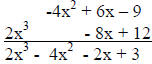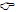Arrange the
terms of each polynomial in descending order with like terms in the same column |
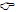| Combine the
terms in each column |
Subtraction of polynomials
The opposite of the polynomial (3x2 – 7x + 8) is –(3x2 – 7x + 8)
To simplify the opposite of a polynomial, change the sign of each term inside of
the
parentheses.
Polynomials can be subtracted using either a horizontal or vertical format. To
subtract, add the
opposite of the second polynomial to the first.
Simplify: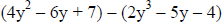 
. Use a
horizontal format.
 |
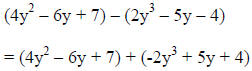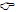Add the
opposite of the second polynomial to the first |
 |
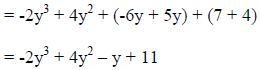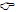Combine like
terms |
Simplify: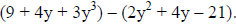 
Use a vertical
format.
The opposite of 2y2 + 4y – 21 is –2y2– 4y + 21
 |
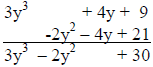Arrange the
terms of each polynomial in descending order with like terms in the same column |
| Note that 4y –
4y = 0, but 0 is not written. |
