Intermediate Algebra Math Review Sheets
1. Solve each formula for the specified variable
I =prt for t
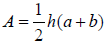 for b
for b
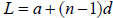 for d
for d
2. Applications
The bus fare in a city is $1.25. People who use the bus have the option of
purchasing a monthly coupon book for $21.00. With the coupon book, the fare is
reduced to $0.50. Determine the number o times in a month the bus must be used
so that the total monthly cost without the coupon book is the same as the total
monthly cost with the coupon book.
Including 8% sales tax, an inn charges $162 per night. Find the inn’s nightly
cost
before the tax is added.
3. Determine whether each relation is a function. Give the domain and the range
for
each relation.
{(3,10), (4, 10), (5, 10)}
{(13, 14), (15, 16), (13, 17)}
4. Find the indicated function value given 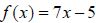
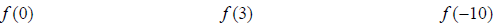

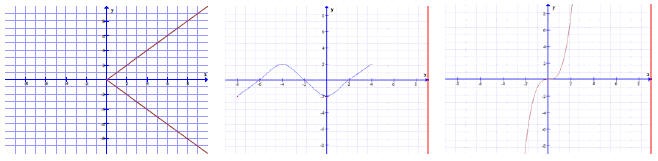
5. Use the vertical line test to identify if each graph is a function or not.
6. Find the domain of the given function. State the domain
in both set builder and
interval notation

Set builder:
Interval:
7. Given

Find each of the following



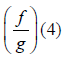 What is the domain of
What is the domain of
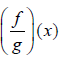
8. Determine the coefficient of each term, the degree of
each term, the degree of the
polynomial, the leading term, and the leading coefficient of the polynomial.
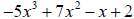
| Term | Coefficient | Degree |
9. Perform the indicated operation (add, subtract or multiply):
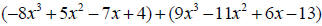
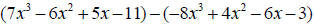


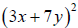
10. Factor






11. Solve for x

12. Find the domain of the given rational function. State
the domain in both set builder
and interval notaion.
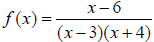
set Builder:
Interval:
13. Simplify:
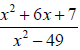
14. Multiply
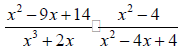
15. Divide
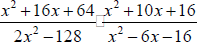
16.Add then simplify
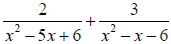
17. Subtract then simplify
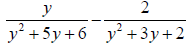
18. Simplify
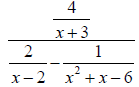
19.Use long division to divide
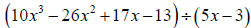
20. Use synthetic division to divide
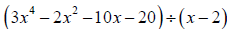
21. Solve
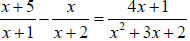
22. Solve for R
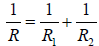
3. Application
Working alone, two people can clean their house in 3 hours and 6 hours
respectively. They have agreed to clean together so that they can finish in time
to
watch a TV program that begins in 1 ½ hours. How long will it take them to
clean the house together? Can they finish before the program starts?
24. Find the indicated root, or state that the expression is not a real number
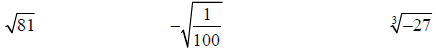
25. Find the indicated function values for the function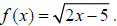 If the
If the
function value is not a real number and does not exist, so state.
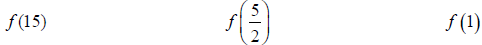
26. Find the domain of the given function. State in set
builder and interval notation.
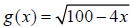
Set Builder:
Interval:
27. Simplify each expression. Assume that each variable
can represent any real number,
include absolute value bars where necessary.
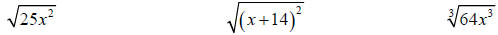
28. Use radical notation to rewrite each expression. Simplify if possible.
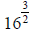
29.Rewrite each expression with rational exponents
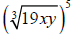
30.Use properties of rational exponents to simplify each expression

31. Use rational exponents to simplify each expression. If
rational exponents appear
after simplifying, write the answer in radical notation.

32. Use the product rule to multiply
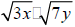
33. Simplify by factoring. Assume that all variables in
radicand represent positive real
numbers
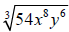
34.Multiply and simplify. Assume that all variables in
radicand represent positive real
numbers
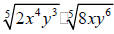
35. Add or subtract as indicated. Assume that all
variables in radicand represent positive
real numbers

36.Simplify by using the quotient rule.
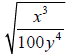
37. Divide and simplify
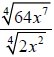
38. Multiply. If possible, simplify any radical expressions that appear in the product.

39. Rationalize the denominator and simplify
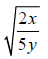
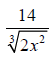
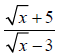
40. Solve the radical equation
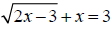
41. Perform the indicated operation. Write the result in the form a + bi

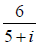
42. Simplify each expression
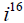
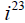
43. Solve by the square room property.
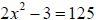
44. Complete the square for the given binomial. Then
factor the resulting perfect square
trinomial.
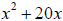
45. Solve by completing the square
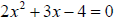
46. Solve by using the quadratic formula
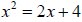
47.Compute the discriminant. Then determine the number and
type of solutions for the
given equation

48. Solve each equation by the method of your choice.
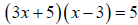
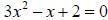
49. Use the vertex and intercepts to sketch the graph of
each quadratic function. Give
the equation for the parabola’s axis of symmetry.
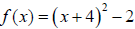 |
 |
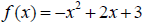 |
 |
50. Application
A model rocket is launched upward from a platform 30 feet above the ground.
he quadratic function 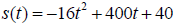 models the rocket’s
height above
models the rocket’s
height above
e ground, s(t), in feet, t seconds after it was launched. After how many seconds
does the rocket reach its maximum height? What is the maximum height?


