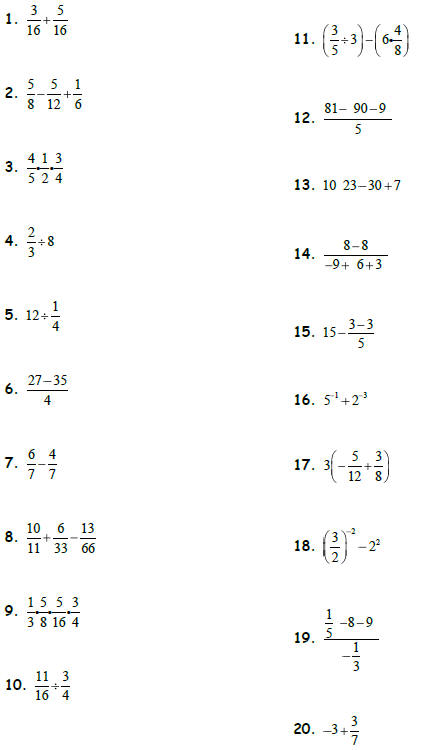Pre-Calculus
Dear 2008-2009 student,
Congratulations on your promotion to Pre-Calculus
and/or
Pre-Calculus Honors.
This packet is due on the first day you return to class in
September.
You will have the opportunity to ask questions about anything in it
when you come back. By the end of the first week of school you will
be given a test on the material from this packet. The test will count
as a first quarter grade and will be used to plan your review and after
school remediation as necessary.
If you need more review over the summer, there are many resources
to be found at the county library and on the Internet. If you find that
you have questions, you can ask them and get additional practice
from “Ask Dr. Math”. You can also view lists of questions previously
asked by other students, with answers provided.
Pre-Calculus Honors, or AP Stats continue the
foundation for our advanced math courses, and we expect a high
level of performance from all students over the coming year. We
expect you to take the initiative to find out about things that you don’t
understand including any information in this packet. The algebra 2
team hopes you enjoy your summer vacation and looks forward to
seeing you in the fall!
Enjoy,
May 2009
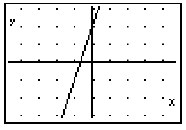
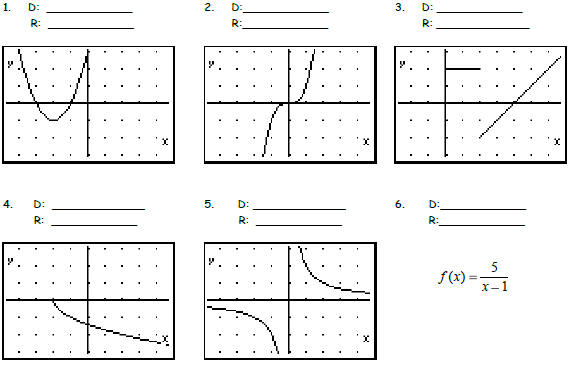
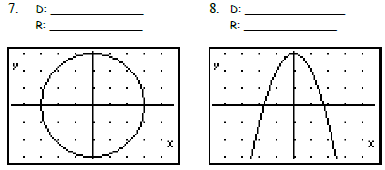
DOMAIN & RANGE
Domain: The possible x-values of a function
Range: The possible y-values of a function
Example:
D: all real numbers
R: all real numbers
Give Domain and Range of the following
FACTORING POLYNOMIALS
When factoring, always try to pull out a greatest common
factor first. Then look for certain patterns
such as the ones shown below:
| Type of factoring: | Examples: |
| Greatest Common Factor: | |
 |
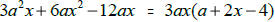 |
| Difference of squares: | |
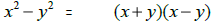 |
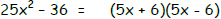 |
| Perfect square trinomials: | |
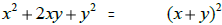 |
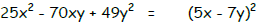 |
| x-squared trinomials: | |
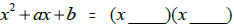 |
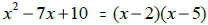 |
To fill in these blanks, find two numbers whose product is ‘b’ and whose sum is
‘a’.
Other trinomials:
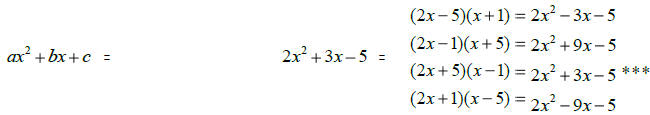
When there is a coefficient other than one
in front of the x2 term, all possibilities need
to be taken into account. These possibilities
are then evaluated by guess and check.
FACTOR COMPLETELY:








RADICAL REVIEW
EXAMPLES:
In order to simplify a radical, look for the highest perfect square
that
is a factor of the radicand ( the number under the radical sign)
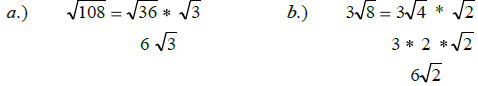
SIMPLIFY:
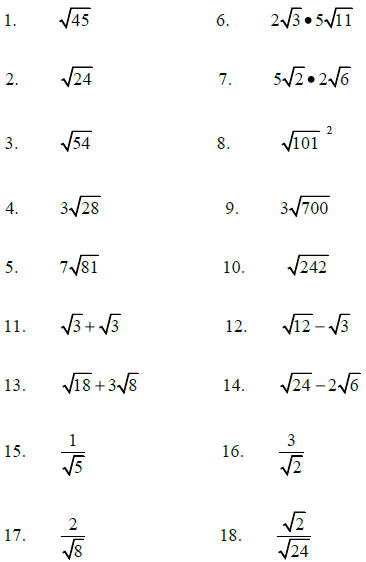
Solve the equations for x:
FUNCTIONS
FUNCTION NOTATION: f(x)
To be written as f(x) means the represented expression satisfies the definition
of a function
--- for each x-value, there is an unique corresponding y-value
Example of function notation: 
EVALUATION OF FUNCTIONS:
f(3) means replace each ‘x’ in f(x) with ‘3’ to find the function’s y-value
EXAMPLE:
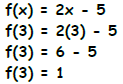
ADDITION, SUBTRACTION AND MULTIPLICATION OF FUNCTIONS:
Functions can be added, subtracted and multiplied just as any other expressions:
EXAMPLE:
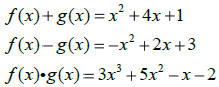
COMPOSITION OF FUNCTIONS:
Composition of functions means instead of replacing ‘x’ in a function with a
number, an entire
function is inserted instead.
EXAMPLE: 
The composition of f(x) and g(x) is written: f (g(x))
To evaluate, simply plug in g(x) wherever an ‘x’ appears in f(x).

PRACTICE PROBLEMS:
Use these functions: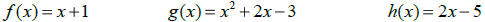







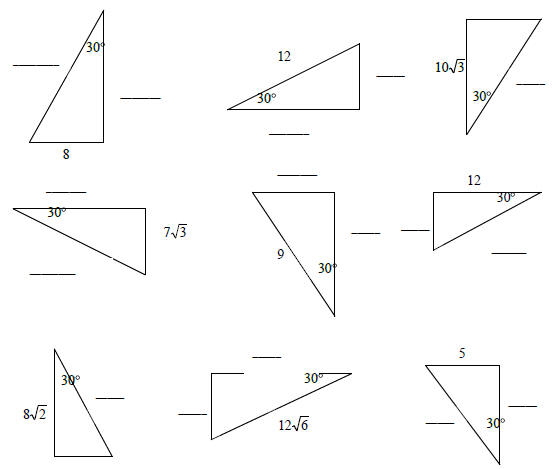
30-60-90 TRIANGLES
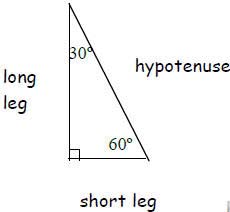
Hypotenuse = twice the short leg
Long Leg = short leg *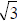
Find the missing sides of the triangles. Each
triangle measures 30-60-90° . Leave answers in
simplified radical form.
45-45-90º TRIANGLES
Hypotenuse = leg *
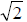
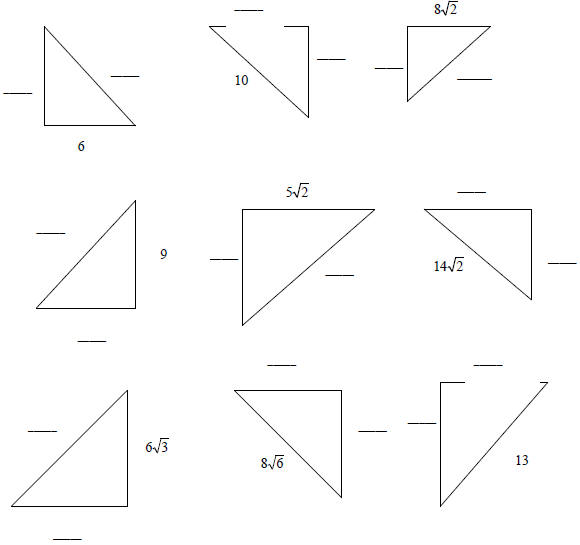
Find the missing sides of the triangles. Each triangle
measures 45-45-90º.
Leave answer in simplified radical form.
SOH-CAH-TOA
Basic Trigonometry Review
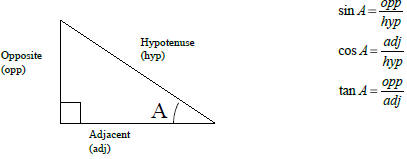
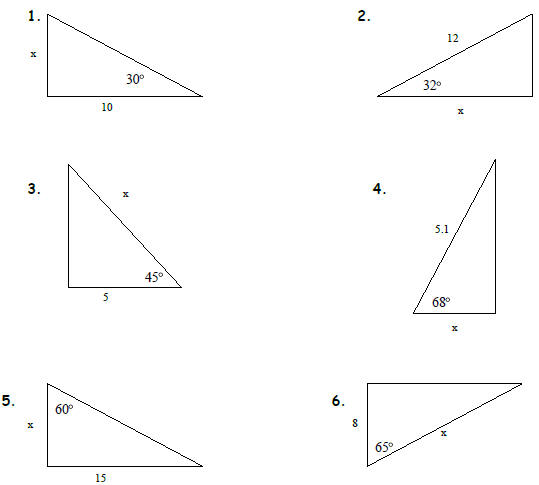
Solve each triangle for the indicated side x.
Arithmetic Review
Evaluate without a calculator. Put answers in simplest form.