Quadratic Functions and Applications
Definition: Quadratic function-A function f is a quadratic
function if
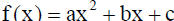
where a, b, and c are real numbers and a is not 0.
The graph is a parabola.
Parabolas are
1. Symmetric about a line (line of symmetry is called the axis)
2. The maximum or minimum point on the curve is called the vertex
Standard curve: f(x)=x2
Graphs to be compared to the standard curve:
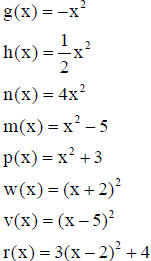
General Principles for Graphs for Quadratic Functions
1. The graph of the quadratic function defined by
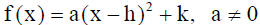
where (h,k) are coordinates of the vertex.
2. The graph opens upward if a is positive and downward if a is negative.
3. The graph is wider than that of 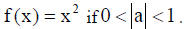 The graph
is narrower than that of
The graph
is narrower than that of
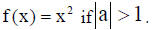
Steps in graphing a parabola:
1. Find the vertex. Find the vertex either by using the formula or by completing
the
square.
2. Select two x coordinates to the left of the vertex and two corresponding
points to
the right of the vertex.
3. Calculate the y coordinates.
4. Plot the points.
Graph the following by selecting at least five points.
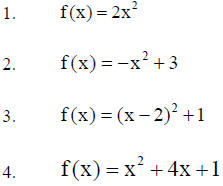
Word Problem
1. Ruth Tynes has 40 yards of fence to enclose a rectangular garden. Find the
dimensions of the rectangle that will give maximum area.
2. A projectile on Earth is fired straight upward so that its distance (in feet)
above
the ground t seconds after firing is given by
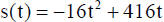
Find the maximum height it reaches and the number of
seconds it takes to reach
that height.


