Math 135 Final Exam Study Guide

Solve the system of equations by substitution.

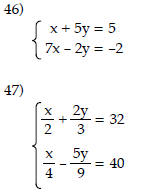
Solve the system of equations.

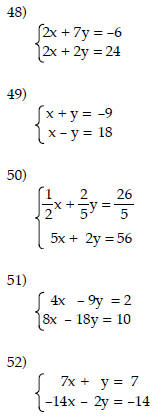
Give the equation of the specified asymptote(s).
53) Vertical asymptote(s):
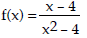
54) Vertical asymptote(s):
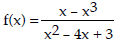
55) Vertical asymptote(s):

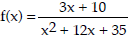
State whether the function is a polynomial function or not. If it is, give its degree. If it is not, tell why not.

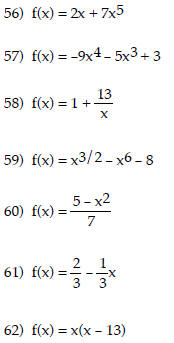
Solve the equation. Find all real solutions.
63) x³ + 2x² - 5x - 6 = 0
64) 2x³ - x² - 10x + 5 = 0

Form a polynomial whose zeros and degree are given.
65) Zeros: 0, - 7, 6; degree 3
66) Zeros: -3, -2, 3; degree 3
67) Zeros: -1, 1, - 5; degree 3

List the potential rational zeros of the polynomial function. Do not find the zeros.
68) f(x) = 5x³ - x² + 3
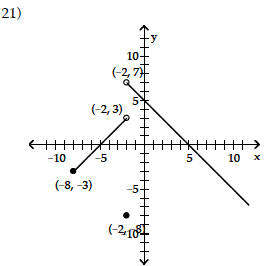
69) f(x) = 6x⁴ + 3x³ - 4x² + 2
70) f(x) = x⁵ - 6x² + 6x + 7

Use synthetic division to find the rmaining zeros of the polynomial.
71) f(x) = x³ - 3x² - 5x + 39; zero: -3
72) f(x) = x³ - 2x² - 11x + 52; zero: -4

Find all of the real zeros of the polynomial function, then use the real zeros to factor f over the real numbers.
73) f(x) = x³ + 2x² - 9x - 18

Find all the (real and complex) zeros of the polynomial function.
74) f(x) = x⁴ - 8x³ + 16x² + 8x - 17

Answer Key
Testname: 135STUDYGUIDE

1) decreasing
(a) (-4, 0.5); (b) (3.5, 6); (c) (-5, -4) U (0.5, 3.5);
(d) (-5, 6); (e) (-3, 2); (f) -3; (g) -1.1; (h) -1.2; 5.2; (i) -1.2; 5.2; (j) 1.4
2) 6
3) - 5
4) 3
5) not a function
6) function
domain: {Bob, Ann, Dave}
range: {Ms. Lee, Mr. Bar}
7) {x|x ≠ -1, 1}
8) all real numbers
9) {x|x ≤ 4}
10) (f + g)(x) = -15x + 13; all real numbers
11) (f + g)(x) = -6x + 8; all real numbers
12) (f - g)(x) = -4x + 1; all real numbers
13) (f - g)(x) = 6x - 1; all real numbers
14) (f · g)(x) = 15x² - 2x - 1; all real numbers
15) (f · g)(x) = 20x² + 52x + 24; all real numbers

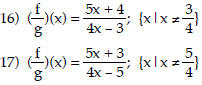
18) function
domain: {x|x ≥ -2}
range: {y|y ≤ 0}
x- intercepts: (-2, 0), (2, 0)
y-intercept: (0, -2)
19) not a function


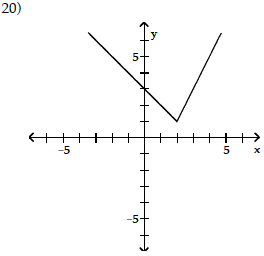
22) 30x + 3
23) 9x + 7
24) 8x² + 4x + 6
25) 8x² + 4x + 5
26) 2x + h - 7
27) 2x + h + 6
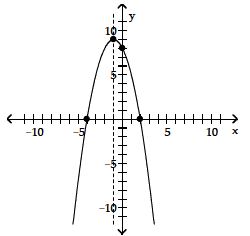
28) vertex (-1, 9)
x-intercepts (2, 0), (- 4, 0)
y-intercept (0, 8)
Axis of symmetry: x = -1

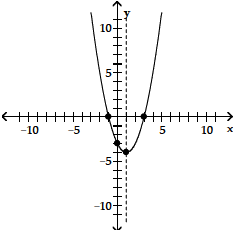
29) vertex (1, -4)
intercepts (3, 0), (- 1, 0), (0, -3)

30) Yes
31) No

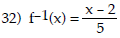
33) Not a one-to-one function

35) 2
36) 3
37) 5
38) 5
39) x > 10
40) x > 8
41) 661 students
42) $6749
43) $2304.54
44) $2854.34
45) $825.81
46) x = 0, y = 1
47) x = 100, y = -27
48) x = 18, y = -6
49) x = 4.5, y = -13.5
50) x = 12, y = -2
51) inconsistent
52) y = -7x + 7, where x is any real number
53) x = 2, x = -2
54) x = 3
55) x = -7, x = -5
56) Yes; degree 5
57) Yes; degree 4
58) No; x is raised to a negative power
59) No; x is raised to non-integer 3/2 power
60) Yes; degree 2
61) Yes; degree 1
62) Yes; degree 2
63) {-3, -1, 2}

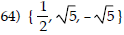
65) f(x) = x³ + x² - 42x for a = 1
66) f(x) = x³ + 2x² - 9x - 18 for a = 1
67) f(x) = x³ + 5x² - x - 5 for a = 1
68) ±1/5,  ±3/5 , ±1,  ±3
69) ±1/6,  ±1/3,  ±1/2,  ± 2/3,  ±1,  ±2
70) ± 1, ± 7
71) 3 + 2i, 3 - 2i
72) 3 + 2i, 3 - 2i
73) -3, -2, 3; f(x) = (x + 3)(x + 2)(x - 3)
74) 1, -1, 4 - i, 4 + i