Moving Straight Ahead Math Background

Solving a Linear Equation

The key to solving equations symbolically is to
understand equality. Many students think of
equality as a signal “to do something.” For
example, students encounter the following:

Students think of an equality as calculating a
set of numbers to get an answer. This can be a
source of many misconceptions. Instead, equality
is a statement that states two quantities are equal.
In this unit, students develop understanding of
equality. Equality can be thought of as a
“balance.” To solve an equation means to
maintain the equality between two quantities.
There are several ways to find the value of a
variable in a linear relationship if the value of the
other variable is known. For instance, in
C = 150 + 10n, where C is the rental cost and n
is the number of bikes, we might want to know
the cost to rent 75 bikes or how many bikes we
can rent for $300. In either case, we are solving for
one of the variables or we are solving a linear
equation with one variable or “one unknown.”
Students can find the value of the variable by
using these methods.

• Solving the equation using symbolic methods.

• Interpreting the information from a table or
graph.

• Reasoning about the situation in verbal
form—“if it costs $10 per bike, then 75 bikes
will cost $750 plus the fixed costs of $150 for a
total of $900.”

Investigation 3 develops symbolic methods for
solving equations. To solve an equation
symbolically, we write a series of equivalent
equations until we have one in which it is easy to
read the value of the variable. Equivalent
equations have the same solutions. Equality or
equivalence can be maintained by adding,
subtracting, multiplying by, or dividing by the
same quantity on both sides of the equation. For
multiplication and division, the quantity must be
nonzero. These procedures are called the
properties of equality.

To help students develop their understanding
of equality, Investigation 3 begins by making the
connection to tables and graphs. Linear equations
can be solved using tables or graphs. For example,
the equation 750 = 150 + 10n is associated with
the related linear function y = 150 + 10x. If
y = 750, then we are looking for a corresponding
value of x. Or, conversely, we can find a
corresponding value of y if we are given a value of
x. At first we expect that students will use graphs
or tables and, in some cases, simply substitute
values into the equation and calculate the missing
value.

Once the concept and properties of equality
have been explored, though, we move to a
pictorial situation to develop a symbolic method
for solving linear equations. First, students explore
adding, subtracting, multiplying, or dividing the
same number to both sides of a numeric sentence:
85 = 70 + 15.

Next, students explore equations like the
following with coins and pouches.

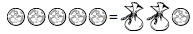
Each pouch in an equation must have the same
number of coins and the number of coins on both
sides of the equality sign are equal.
Students can solve this by taking 1 coin from
each side. This leaves 4 coins on the left and
2 pouches on the right. Because each pouch must
have the same number of coins, students can
intuitively divide both sides by 2 to find that each
pouch contains 2 coins. This provides a transition
to the more abstract situations of solving linear
equations in one unknown. Students first find the
number of coins using the pictures. Then they
translate each picture into a symbolic statement.
For example, if x represents the number of coins
in a pouch, then the preceding pictorial statement
can be represented as 5 = 2x + 1. Next, students
apply the properties of equality to isolate the
variable—that is, they solve the equation for x.
The set of equations is selected carefully to allow
students an opportunity to look at what each
symbolic statement means.
In this unit, we solve the following types of
equations:

6 - 3x = 10
5 + 17x = 12x – 9
2(x + 3) = 10

Integers and the distributive property were
developed in Accentuate the Negative. Review of
integers and the distributive property are
provided in the Connections section of each ACE.

Solving a System
of Two Linear Equations

Students informally solve systems of linear
equations throughout the unit. They use graphs
and tables to find the point of intersection of two
lines. For example, a problem in Investigation 1
has students comparing pledge plans. Students are
asked to determine if any of the two pledge plans
will have the same amount of money.



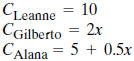
C represents the amount of money collected
for x kilometers.

To find the number of kilometers that make
two plans equal, students start by using tables or
graphs. Later, students can solve two of the
preceding equations symbolically. To find when
Gilberto’s plan equals Alana’s plan, they write
2x = 5 + 0.5x and solve for x.

This can be done for either of the two plans.
From the graphs of the three plans, students note
that all three plans will never have the same costs
for a given amount of kilometers. In Investigation
3, students learn that situations like this one
represent a system of linear equations. Without
calling attention to it, students solve a linear
system by finding the point of intersection of the
two lines symbolically. They find the x value when
the y values are equal or by setting the two
equations equal. Students can also use a table or
graph to find the point of intersection.

It is important that students understand what a
solution is, whether they are dealing with a
symbolic solution or a graphical solution, and that
they can connect these two views of a solution.
Thus, 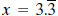is a solution for 2x = 5 + 0.5x. It
means that if Gilberto and Alana each walk
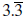kilometers, they earn the same amount.
Graphically, the lines y = 2x and y = 5 + 0.5x
intersect at 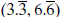.This solution means that
when they each walk 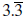kilometers, they each
earn about $6.67.

Ideas about inequality are informally explored
by asking questions like: “if x = 4, does Gilberto
earn more or less than Alana?” Students can
answer this question by finding the missing
coordinate in 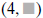for each equation, y = 2x
and y = 5 + 0.5x and then comparing the
coordinates. In the Shapes of Algebra unit,
students explore linear inequalities and systems of
linear equations in depth.

Finding the Equation of a Line
In this unit, most of the linear equations are of the
form y = mx + b. In some situations, equations
can be obtained by translating the verbal situation
directly into symbols.
To find the equation of a line symbolically, we
find the slope of the line (coefficient of x) and the
y-intercept (the constant term b) and substitute
these values into the equation y = mx + b.
Students are given one of the following pairs of
information about a line:

• The slope and y-intercept

• The slope and a point on the line

• Two points on a line

In the first case, the values are substituted
directly into the equation y = mx + b. In the
second case, the slope is substituted into the
equation y = mx + b and the coordinates of the
point are substituted into the equation to find the
y-intercept. In the third case, the slope is
determined using two points and then another
point is used to find the y-intercept.The following
methods can be used to find the y-intercept of a
line.

Method 1:
Finding the y-Intercept Symbolically

First, find the slope of the line.
Given the two points, (1, 4) and (3, 10), the
slope is 3.
Then substitute the slope into the equation
y = mx + b to obtain y = 3x + b. Since both
points lie on the line, the x and y values of the
points satisfy the equation. Choose one point
[(1, 4)] and substitute it into the equation.

4 = 3(1) + b

Solving for b, b = 1.
Now substitute for b.

y = 3x + 1

This is the equation of the line that passes
through the points (1, 4) and (3, 10).

Method 2:
Finding the y-Intercept Using a Table

Some students prefer to find the y-intercept using
a table and working backwards. Consider the
following table.

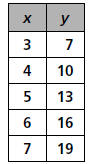
First, students note that this is a linear
relationship because as x increases by 1 unit, y
increases by 3 units. So, the slope is 3.To find the
y-intercept, they work backwards using the slope.
That is, as x decreases by 1 unit, y decreases by
3 units. This is repeated until x = 0.

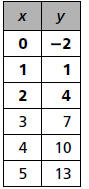
The y-intercept is -2 and the equation of the
line is y = 3x - 2. Some students have a strong
sense of the y-intercept as a starting point, to
which you repeatedly add a constant number to
generate the table.

Method 3:
Finding the y-Intercept Using a Graph

Students also use a graph to find the y-intercept.
They extend the line to intercept the y-axis. Some
use the ratio definition of slope to work from a
point on the graph backward or forward until they
hit the y-axis.