LINEAR ALGEBRA AND DIFFERENTIAL EQUATIONS
Objectives: To study both the computational use of
matrices and their connection
with vector spaces; to use this understanding to understand the theory of
differential
equations; and to develop and apply various techniques for solving these
equations.
Subject material
A differential equation is an equation involving an unknown function and its
various derivatives.
You studied the simplest sort of these in calculus: “Solve
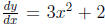 ” is another
” is another
way of saying “Calculate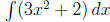 ”.
”.
Like integrals, differential equations are intrinsically “hard”, in the sense
that there is no
systematic procedure which will produce explicit solutions to all of them. But
certain types
which arise frequently in practice can be solved explicitly, and one of our
major goals for the
course is to learn some of the fundamental techniques.
We will begin with a recap and more thorough examination of where MAT110 leaves
off: with a few examples of how differential equations arise in practice, how we
can gain a
qualitative understanding of them using slope fields, and how we can explicitly
solve some
of them using separation of variables.
We will see along the way that we frequently need to solve systems of linear
equations.
We will also see that the general solution of an nth order differential equation
typically has n
“degrees of freedom” associated with it. These two observations lead us to two
of the central
subjects in linear algebra: Matrices encapsulate the computational side of
solving equations,
and the concept of vector spaces formalizes the geometry and algebra of our
“degrees of
freedom”. We will study both topics fairly extensively in their own right.
Next we will survey a few particular solution techniques for first-order DEs and
some of
their applications. The linear algebra will lurk in the background for a while,
until it reappears
more essentially when we finish the course with higher order systems.
I expect that we will cover most of the topics in the first six chapters of
Peterson and
Sochacki’s book, with occasional digressions for perspectives (especially
geometric ones)
other than theirs. The goal of learning differential equations and linear
algebra in a single
course is an ambitious one, and we will move quickly. It is very important that
you not fall
behind.
Assignments and grades
Assignments: If you’ve made it this far in mathematics, you know the
importance of
practice. Problem sets will form a very substantial part of your grade – both in
themselves,
and because they form the foundation of learning for the exams. I encourage you
to discuss
the problems with me, each other, and the tutors. But you should write your
final solutions
on your own, without consulting anything more than sketchy notes that you
understand
thoroughly. Submitting someone else’s work as your own is plagiarism. It is
unethical and
educationally counterproductive.
I will assign problem sets regularly and collect and grade your accumulated
solutions every
week or so. Some exercises will be routine practice, some more theoretical, and
occasionally
some may be designed to guide you in a more thorough exploration in a topic than
we have
time for in the classroom or on exams. Please put your name on every page, write
neatly,
label each problem, and staple your pages together in order. Leave margins with
room for
comments and corrections.
Your first assignment is easy: Sometime during the first week of class
(by January 28,
to be specific), come to my office and ask me a question about mathematics. It
can be
anything – course work, general curiosity, long division, the theological
significance of the
 incompleteness theorem... – my main
objective is to encourage open dialogue from
incompleteness theorem... – my main
objective is to encourage open dialogue from
the very beginning. I’ll also ask you about your mathematical (and related)
background,
and what kind of things I can do to make the course go well for you. (I know
many of you
from earlier courses, and look forward to the chance to say hello again. Welcome
back! )
Exams: We will have two midterm exams in class, tentatively on
February 27 and April
10, and a three-hour cumulative final to be scheduled by the registrar during
finals week,
May 5 – 9.
Exams will include a mix of very routine computational problems and
applications, and
more abstract and conceptual ones.
Grades: You will be assigned a percentage grade based on the following
weighted ingredients:
| First (office-visiting) assignment: | 2% |
| Homework assignments: | 33% |
| First midterm | 20% |
| Second midterm | 20% |
| Final Exam | 25% |
| Total | 100% |
Your percentage grade will then be converted to a letter
grade using an increasing function.
(Grades in the 90s will correspond roughly to the A range; 80s, the B range; and
so forth,
subject to some fine tuning at the end.)
Calculators and computers. I will not require it, but you may find it
useful to have a
calculator which graphs and numerically integrates functions. But be aware that
we will also
work without calculators on a regular basis, and possibly on some exams.
We will use a java-based slope field viewer which I will direct you to on the
web page.
We may also occasionally make use of Mathematica, a powerful computer program
for doing
mathematics. Mathematica is available on the F&M software server, so feel free
to take a
look at it and explore its capabilities. Many of you will have seen it in
calculus 3; if and
when we do use it, I will provide instructions.
Finally, course materials will be posted on the web, and we will use email and
eDisk for
communication outside of class. Please check your email regularly.
Attendance: I expect you to attend class every day, and you will be held
accountable for
everything said and done in class. When you are in class, you should be there
mentally as
well as physically. This means you should be alert, have done the reading, and
be prepared
to ask questions and work effectively.
I do not intend to take attendance explicitly, but if you are repeatedly absent,
I will contact
you to see whether there is a problem I can help you solve. If excessive
absences persist, I
may assess a grade penalty.
Missing exams: Do not miss exams. Rescheduling exams is difficult and
disruptive, and
will only be considered with persuasive documentation from Dean O’Day or Appel
Health
Services.
Contacting me and getting help
Every mathematician finds work at some level difficult – it is normal to get
stuck sometimes.
I hope you feel comfortable asking me for help.
If you are standing right in front of me, it is easy to contact me. If you are
not, then you
can either find me (thereby reducing the problem to one you know how to solve),
send me
email, or call me.
Finding me: I will be in my office and happy to talk to you during my
office hours, and
often at other times as well – including evenings, sometimes. If my door is
open, please come
in.
Email: I use it, and it is probably the most reliable way to get in touch
with me.
Phone: I use it, too. Have been for years. My office phone number is
358-7163, or just
extension 7163 on campus. My home phone number is 391-2944, but please save that
for
emergencies.
Other help: The Mathematics Department also has student tutors available.
They generally
work 3:00 – 6:00 and 7:00 – 10:00, Sundays through Thursdays, beginning in the
second
week of classes. I will notify you of the precise rooms and schedule when they
are determined.
Please note: only some of the tutors have enough expertise to help with advanced
classes.
The schedule should indicate which is which.
Last words
Curiosity above and beyond the call of duty is strongly encouraged. Honesty is
required.
Help is available. Good luck.


