Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Solve quadratic equations

1 (a) Solve the quadratic equation

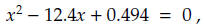
by evaluating the quadratic formula using three-digit decimal arithmetic and
rounding. The exact roots rounded to 6 digits are 0.0399675 and 12.3600.

(b) You should observe loss of significance in one of your computed zeros of
part (a). If we consider the 6-digit answers provided as the “true” ones, what is
this solution’s relative error? Following Definition 2.2 in Kharab & Guenther
(p. 33), to how many significant digits does your computed root approximate
the true one? Explain what aspect of the coefficients in the quadratic equation
to be solved led to this loss of significance.

(d) While there is loss of significance in one solution of the quadratic equation in (a),
it does not occur in the other. Write an Octave/Matlab function which accepts
as a vector [ a b c] the coefficients of a quadratic function f (x) = ax^2 + bx + c,
computes the root that has larger absolute value, and then obtains the other
root using the formula in part (c). You may assume that the roots are distinct
real numbers—i.e., that b^2 - 4ac > 0. (Hand in a printout of your function.)

(e) As in part (a), use 3-digit decimal arithmetic to solve the quadratic equation

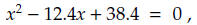
whose exact roots rounded to 6 digits are 6.00000 and 6.40000. You should once
again observe loss of significance. Does our method in part (d) for dealing with
loss of significance help here? If not, what aspect of this situation makes it
different?

2.2.5 If x₁, x₂ are approximations to X₁, X₂ with errors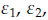 show that the relative error

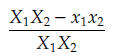
of the product X₁X₂ is approximately the sum

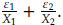
2 In class we showed that, under suitable assumptions on f and h, we have

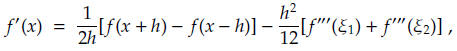
where 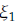lies between x and x + h, and 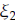lies between x and x - h.

(a) What, exactly, are these assumptions on f and h?

(b) Supposing that f''' is suitably continuous, show that the truncation error term
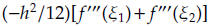may be replaced by a single term 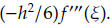(Hint.
Use the IVT.) In what interval could we assume this new number resides?

9.1.3 Derive the following approximate formulas.

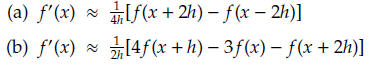
9.1.3 Use Taylor’s series to derive the following approximation formul for the first derivative
of f .

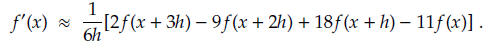
9.1.9 Show that the approximation formula in Exercise 9.1.8 has an error of O(h^3).

Home