Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Math Scope and Sequence Grade 8

Standards
NCTM Curriculum Focal Points
The National Council of Teachers of Mathematics (NCTM) created its Curriculum Focal Points for Prekindergarten through Grade 8 Mathematics (2006) to provide
descriptions of the most significant mathematical concepts and skills at each grade level. These focal points were chosen according to three criteria: they are
mathematically important, both for further study in mathematics and for use in applications in and outside of school; they conform to what is known about learning
mathematics; they connect logically with the mathematics in earlier and later grade levels. According to the NCTM, “these curriculum focal points should be considered
as major instructional goals and desirable learning expectations, not as a list of objectives for students to master.” It is important that none of the focal points be omitted;
it is less important whether they are addressed a year earlier or later, or over a period of two years, compared with the suggested sequence in the document.
On this page, each of the NCTM focal points is followed (in parentheses) by the corresponding New York State performance indicators.

Focal Points
Algebra: Analyzing and representing linear functions and solving linear equations and systems of linear equations
Students use linear functions, linear equations, and systems of linear equations to represent, analyze, and solve a variety of problems. They recognize a proportion (y/x =
k, or y = kx) as a special case of a linear equation of the form y = mx + b, understanding that the constant of proportionality (k) is the slope and the resulting graph is a
line through the origin. Students understand that the slope (m) of a line is a constant rate of change, so if the input, or x-coordinate, changes by a specific amount, a, the
output, or y-coordinate, changes by the amount ma. Students translate among verbal, tabular, graphical, and algebraic representations of functions (recognizing that
tabular and graphical representations are usually only partial representations), and they describe how such aspects of a function as slope and y-intercept appear in
different representations. Students solve systems of two linear equations in two variables and relate the systems to pairs of lines that intersect, are parallel, or are the
same line, in the plane. Students use linear equations, systems of linear equations, linear functions, and their understanding of the slope of a line to analyze situations
and solve problems. (7.A.7-8, 7.A.10)

Geometry and Measurement: Analyzing two- and three-dimensional space and figures by using distance and angle
Students use fundamental facts about distance and angles to describe and analyze figures and situations in two- and three-dimensional space and to solve problems,
including those with multiple steps. They prove that particular configurations of lines give rise to similar triangles because of the congruent angles created when a
transversal cuts parallel lines. Students apply this reasoning about similar triangles to solve a variety of problems, including those that ask them to find heights and
distances. They use facts about the angles that are created when a transversal cuts parallel lines to explain why the sum of the measures of the angles in a triangle is 180
degrees, and they apply this fact about triangles to find unknown measures of angles. Students explain why the Pythagorean theorem is valid by using a variety of
methods—for example, by decomposing a square in two different ways. They apply the Pythagorean theorem to find distances between points in the Cartesian
coordinate plane to measure lengths and analyze polygons and polyhedra. (5.G.7-8, 7.G.5-9)

Data Analysis and Number and Operations and Algebra: Analyzing and summarizing data sets
Students use descriptive statistics, including mean, median, and range, to summarize and compare data sets, and they organize and display data to pose and answer
questions. They compare the information provided by the mean and the median and investigate the different effects that changes in data values have on these measures
of center. They understand that a measure of center alone does not thoroughly describe a data set because very different data sets can share the same measure of center.
Students select the mean or the median as the appropriate measure of center for a given purpose. (6.S.2, 6.S.4-8, 7.S.1-6)

Connections to the Focal Points

Algebra: Students encounter some nonlinear functions (such as the inverse proportions that they studied in grade 7 as well as basic quadratic and exponential functions)
whose rates of change contrast with the constant rate of change of linear functions. They view arithmetic sequences, including those arising from patterns or problems,
as linear functions whose inputs are counting numbers. They apply ideas about linear functions to solve problems involving rates such as motion at a constant speed.
Geometry: Given a line in a coordinate plane, students understand that all “slope triangles”—triangles created by a vertical “rise” line segment (showing the change in
y), a horizontal “run” line segment (showing the change in x), and a segment of the line itself—are similar. They also understand the relationship of these similar
triangles to the constant slope of a line.
Data Analysis: Building on their work in previous grades to organize and display data to pose and answer questions, students now see numerical data as an aggregate,
which they can often summarize with one or several numbers. In addition to the median, students determine the 25th and 75th percentiles (1st and 3rd quartiles) to obtain
information about the spread of data. They may use box-and-whisker plots to convey this information. Students make scatterplots to display bivariate data, and they
informally estimate lines of best fit to make and test conjectures.
Number and Operations: Students use exponents and scientific notation to describe very large and very small numbers. They use square roots when they apply the
Pythagorean theorem.

Academic Language
Grade 8 Mathematical Language

PreK-8 Glossary of Mathematical Terms

Development of Content Topics and Concepts
For each content strand these documents trace the development year by year of every band (i.e., sub-skill) from elementary school through high school. As such they
provide insight into the foundational work done in previous grades and map the subsequent elaboration of the topics in later courses.
Band Traces:
The chart below depicts the number of performance indicators for the content strands by grade level. The emphasis in grades Pre-Kindergarten-4 is on Number Sense
and Operations. Algebra builds slowly beginning with patterns in the early elementary grades and leads up to relations and functions in grade 8. Geometry builds as well
with a heavy emphasis in the grades 5-8. Measurement increases significantly across the grades with the exception of grade 8. Statistics includes the collection and
display of data in the early elementary grades and probability is introduced in grade 5.

Number of Content Performance Indicators by Grade Level
Content Strand	Pre-K	K	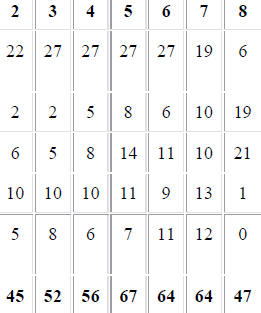TOTAL
Number Sense and Operations Algebra	9 1	13 2	207 56
Geometry Measurement	2 2	5 3	87 80
Statistics and Probability TOTAL	4 18	5 28	67 497

Mathematics Scope and Sequence – Middle School
Grade 8

	September-October	November-December	January- March	Post-March
N U M B E R S E N S E A N D O P E R A T I O N S S T R A N D	Operations 8.N.3 Read, write, and identify percents less than 1% and greater than 100% 8.N.4 Apply percents to: Tax, percent increase/decrease, simple interest, sale price, commission, interest rates, and gratuities Estimation 8.N.6 Justify the reasonableness of answers using estimation	Operations 8.N.1 Develop and apply the laws of exponents for multiplication and division 8.N.2 Evaluate expressions with integral exponents 8.N. 3 Read, write, and identify percents less than 1% and greater than 100% 8.N.4 Apply percents to: Tax, percent increase/decrease, simple interest, sale price, commission, interest rates, and gratuities Estimation 8.N.6 Justify the reasonableness of answers using estimation	Operations 8.N.4 Apply percents to: Tax, percent increase/decrease, simple interest, sale price, commission, interest rates, and gratuities Estimation 8.N.5 Estimate a percent of a quantity, given an application


A L G E B R A S T R A N D	Variables and Expressions 8.A. 3 Describe a situation involving relationships that matches a given graph 8.A.4 Create a graph given a description or an expression for a situation involving a linear or nonlinear relationship Patterns, Relations and Functions 8.A.15 Understand that numerical information can be represented in multiple ways: arithmetically, algebraically and graphically 8.A.16 Find sets of ordered pairs to satisfy an algebraic expression and then plot the ordered pairs and draw the line	Variables and Expressions 8.A.5 Use physical models to perform operations with polynomials (uses area of rectangles as a way to think about the distributive property) 8.A.6 Multiply and divide monomials 8.A.7 Add and subtract polynomials (integer coefficients) 8.A.8 Multiply a binomial by a monomial or binomial (integer coefficients) 8.A.9 Divide a polynomial by a monomial (integer coefficients) Equations and Inequalities 8.A.12 Apply algebra to determine the measure of angles formed by or contained in parallel lines cut by a transversal and by intersecting lines	Variables and Expressions 8.A.1 Translate verbal sentences into algebraic inequalities 8.A. 2 Write verbal expressions that match given mathematical expressions 8.A.3 Describe a situation involving relationships that matches a given graph 8.A.5 Use physical models to perform operations with polynomials 8.A.10 Factor algebraic expressions using the GCF 8.A.11 Factor a trinomial in the form ax²+bx+c; a=1 and c having no more than 3 sets of factors Equations and Inequalities 8.A.13* Solve multi-step inequalities and graph the solution set on a number line 8.A.14* Solve linear inequalities by combining like terms, using the distributive property, or moving variables to one side of the inequality (include multiplication or division of inequalities by a negative number) Patterns, Relations and Functions 8.A.15 Understand that numerical information can be represented in multiple ways: arithmetically, algebraically and graphically	Patterns, Relations and Functions 8.A.17* Define and use correct terminology when referring to function (domain and range) 8.A.18* Determine if a relation is a function 8.A.19* Interpret multiple representations using equation, table of values and graph


G E O M E T R Y S T R A N D	Geometric Relationships 8.G.1 Identify pairs of vertical angles as congruent 8.G.2 Identify pairs of supplementary and complementary angles 8.G.3 Calculate the missing angle in a supplementary or complementary pair 8.G.4 Determine angle pair relationship when given two parallel lines cut by a transversal 8.G.5 Calculate the missing angle measurements when given two parallel lines cut by a transversal 8.G.6 Calculate the missing angle measurements when given two intersecting lines and an angle Coordinate Geometry 8.G.13* Determine the slope of a line from a graph and explain the meaning of slope as a constant rate of change 8.G.14* Determine the y-intercept of a line from a graph and be able to explain the y-intercept 8.G.15* Graph a line using a table of values 8.G. 16* Determine the equation of a line given the slope and the y-intercept 8.G.17* Graph a line from an equation in slope-intercept form (y= mx + b)		Transformational Geometry 8.G.7 Describe and identify transformations in the plane, using proper function notation (rotations, reflections, translations, and dilations.) 8G.8 Draw the image of a figure under rotations of 90 and 180 degrees 8.G.9 Draw the image of a figure under a reflection over a given line 8.G.10 Draw the image of a figure under a translation 8.G.11 Draw the image of a figure under a dilation 8.G.12 Identify the properties preserved and not preserved under a reflection, rotation, translation, and dilation Coordinate Geometry 8.G.18* Solve systems of equations graphically (only linear, integral solutions, y=mx +b format, no vertical or horizontal lines) 8.G.19* Graph the solution set of an inequality on a number line 8.G.20* Distinguish between linear and nonlinear equations ax²+bx+c; a=1 (only graphically) 8.G.21* Recognize the characteristics of quadratics in tables, graphs, equations, and situations	8.G.0Construct the following using a straight edge and compass: Segment congruent to a segment; angle congruent to an angle; perpendicular bisector, and angle bisector Coordinate Geometry* 8.G.20* Distinguish between linear and nonlinear equations ax²+bx+c; a=1 (only graphically) 8.G.21* Recognize the characteristics of quadratics in tables, graphs, equations, and situations

M E A S U R E M E N T S T R A N D			Units of Measurement 8.M.1 Solve equations/ proportions to convert to equivalent measurements within metric and customary measurement systems.

Home