Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Entry Level Skills

Entry Level Skills for College Preparedness in College Algebra

A majority of the math departments in Missouri two-year institutions identified the following skills as necessary for entrance into college-level math. All of these entry-level skills are not necessarily expected to be mastered. However, College Algebra instructors expect the student to be able to perform these skills with a minimal amount of review.

1. Utilize commutative, associative, and distributive properties and simplify expressions using the order of operations
{Ex: -3 - (4² - 2) - 10 / (2+3) }

2. Distinguish between elements of the sets of real numbers
{Ex: Integers vs num} Rationalbers

3. Distinguish between expressions, equations, and different types of equations

4. Solve linear equations and inequalities
{Exs:2(x-3)=4x+1; 3x-2 ≤ 4(x-3)}

5. Solve absolute value equations and inequalities (graph the solution on a number line and express answer in interval notation)
{Exs: | 3x-4 | +7 = 10; | 4x-5 | - 3 < 7 }

6. Solve systems of equations and label them as consistent, inconsistent, or dependent
{Ex: Solve: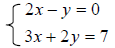

7. Simplify exponential expressions including scientific notation
{Exs: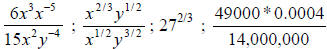(work in scientific notation)}

8. Use terminology of polynomials including but not limited to leading coefficient, term, constant, equation, expression, and degree
{Exs: Write a 3<sup>rd</sup> degree equation containing 3 terms with a leading coefficient of -2 and a constant of -6. }
9. Perform operations with polynomials including addition, subtraction, multiplication, squaring, and division
{Exs: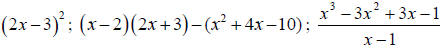(using synthetic division) }

10. Solve quadratic equations by factoring and quadratic formula

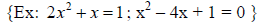
11. Perform operations with rational expressions including addition, subtraction, multiplication, and division

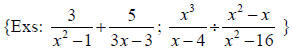
12. Solve rational equations and recognize undefined variable values

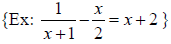
13. Perform operations with terms containing radicals including addition, subtraction, multiplication, and division

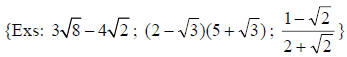
14. Solve equations containing radicals

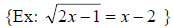
15. Perform fundamental graphing skills including graphing linear equations and inequalities, calculating slope, finding intercepts of a line, and finding the equation of a line that satisfies given information
{Exs: find slope, distance and midpoint given 2 points (-3,5) and (2,1); graph linear equations and inequalities
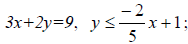write the equation of a line parallel (or perpendicular) to y=3x+1 through (2,4) }

16. Evaluate functions in function notation, graph linear and quadratic functions, find range and domain (50% of community colleges)
{Exs: find f(-2) given f(x) = x<sup>3</sup> - 2x² - 4x + 6; graph and find range and domain given the function f(x)=x²-2

17. Perform elementary operations on a graphing calculator including +, - ,*, /, powers and graphing simple functions in the standard window

18. Translate and solve application problems including the ability to:
• Solve formulas for a specified variable
{ Ex: Solve A = P + Prt , for P }
• Recognize geometry terms and apply geometric concepts
A landscaper, who just completed a rectangular flower garden measuring 6 feet by 10 feet, orders 1 cubic yard of concrete, all of which is to be used to build a border of uniform width around the outside of the garden. If the border is to have a depth of 3 inches, how wide will the border be?
• Work interest and investment problems
Candy has $70,000 to invest and requires an overall rate of return of 9%. She can invest in a safe, government-insured certificate of deposit, but it only pays 8%. To obtain 9% she agrees to invest some of her money in noninsured corporate bonds paying 12%. How much should be placed in each investment to achieve her goal?
• Work mixture problems
How much water should be added to a gallon of antifreeze to obtain a 60% antifreeze solution?
• Work motion problems
Tanya, who is a long-distance runner, runs at an average velocity of 8 mph. Two hours after Tanya leaves your house, you leave in your car following the same route traveling at 35 mph. How long until you pass her and how far from home will you be?
• Work application problems involving work rates
An inlet can fill a tank in 4 hours and the outlet can empty the tank in 10 hours. How long will it take to fill the tank if the outlet is accidentally left open?
• Verbalize mathematical procedures using correct terminology and symbols

Home