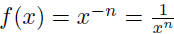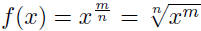Functions
| Announcements • Homework 2 due this Friday in class. – Please write your Section number on your homework. – Staple pages together. • Two volunteer note takers needed. |
| Recall: •A function f is a rule that assigns to each element x of a set X a unique element y of a set Y . f (x) = y •The element y is called the image of x under f and is denoted f (x). The set X is called the domain of f, and the set of all images of elements of X is called the range of the function. •If the range of f consists of all of Y , then f is said to map X onto Y . If each element in the range is the image of one and only one element in the domain, then f is said to be a one-to-one function. •A function f is bounded on [a, b] if there exists a number B such that |f (x)| ≤B for all x in [a, b]. •y is called the dependent variable and x is called the independent variable. |
| Domain Convention • Domain of f is assumed to be the set of real numbers for which the function is defined (unless otherwise specified). • Examples: find the domain: 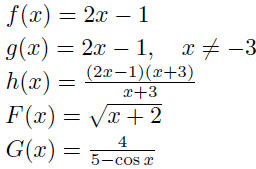 |
| Function equality • Two functions f and g are equal if and only if 1. f and g have the same domain 2. f (x) = g (x) for all x in the domain • Example: 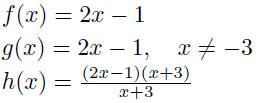 |
| Function composition The composite function f o g is defined by
for each x in the domain of g for which g (x) is in
the domain of f.
We can also express a given function as a
composition of two
|
| Example application Suppose a study showed that when the population is p hundred thousand people, the average daily level of carbon monoxide in the air is given by
parts per million (ppm).
hundred thousand people.
|
| • The graph of a function consists of points
whose coordinates (x, y) satisfy y = f (x), for all x in the domain of f. • Vertical line test for function • Intercepts of a graph: y-intercept is the point (0, b) where b = f(0). An x-intercept is a point (a, 0) where f (a) = 0. • Note that there can be at most one y-intercept. There may be more than one x-intercept. • To find x-intercepts, solve f (x) = 0 for x. • To find y-intercept, calculate f(0) (if 0 is in the domain). |
| Symmetry • symmetric with respect to the y-axis: f(−x) = f (x) (even function) Examples: f (x) = cos x, f (x) = x2 • symmetric with respect to the origin: f(−x) = −f (x) (odd function) Examples: f (x) = sin x, f (x) = x3 • Some functions are even, some are odd, some are neither. • See sample graphs in Table 1.3. |
| Classification of Functions Algebraic functions: • Polynomial:
• an is the leading coefficient |
| • A rational function is the quotient of two
polynomial functions, p (x) and q (x),
• Power functions: f (x) = xr (r nonzero, real) |
| Transcendental functions: • Trigonometic functions: f (x) = cos x • Exponential functions: f (x) = b x • Logarithmic functions: 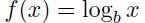 |
| Section 1.4: inverse functions • 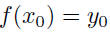 • If f has an inverse f -1, it is the function that reverses the effect of f: 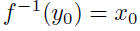 • If the inverse of a function is itself a function, we have the following definition: Let f be a function with domain D and range R. Then the function f -1 with domain R and range D is the inverse of f if 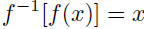 for all x in D for all x in Dand 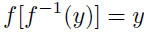 for all y in R for all y in R• If f has an inverse, the inverse is unique. |
| • Not every function has an inverse. (E.g., f (x)
= x2.) • A function f will have an inverse f -1 on the interval I when there is exactly one number in the domain associated with each number in the range. • I.e., a function has an inverse only if it is one-to-one. • “Horizontal line test” |
| • A function is strictly increasing on an
interval I if its graph is always rising on I 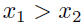 implies implies
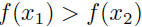 • A function is strictly decreasing on an interval I if its graph always falls on I 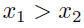 implies implies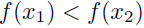 • A function is strictly monotonic on an interval I if it is either strictly increasing or strictly decreasing throughout that interval. Theorem: A strictly monotonic function has an inverse. Lef f be a a function that is strictly monotonic on I. Then f -1 exists and is strictly monotonic on I (strictly increasing if f is strictly increasing and strictly decreasing if f is strictly decreasing). |
| Graphing inverse functions • If (a, b) is a point on the graph of f, then (b, a) is a point on the graph of f -1. • You can graph f -1 by reflecting the graph of f about the line x = y |
| Inverse Trig Functions • The trigonometric functions are not one-to-one, so they do not in general have inverses. • But we can restrict them to intervals on which they are one-to-one and do have inverses. • E.g., sin (x) is strictly increasing on 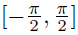 . If we restrict . If we restrictsin (x) to that interval, it does have an inverse, sin -1. 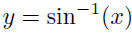 if and only if x = sin (y) and if and only if x = sin (y) and
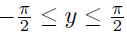 • Similar process for the other trigonometric functions. See Table 1.4 in Strauss. |
| Inversion Formulas • 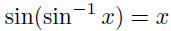 for for
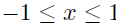 • 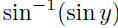 for for
• 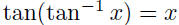 for all x for all x• 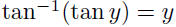 for for
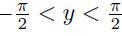 |



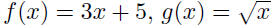
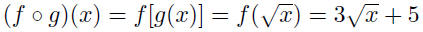
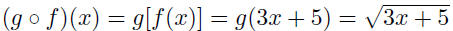
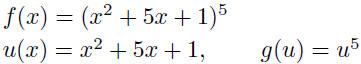
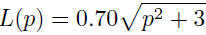
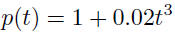
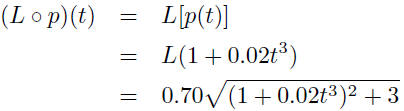
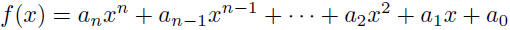
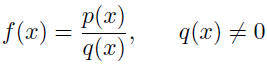
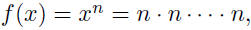 (pos. integer n)
(pos. integer n)