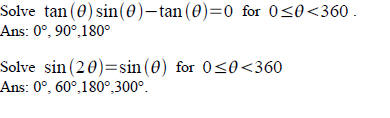MATH 1450 Chapter 6 Review
1 Fundamental Identities
Tool: Identities are true for all values of angle θ
and are
grouped into categories. They may be used to simplify
expressions.
Reciprocal Identities:
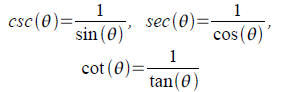
Quotient Identities:
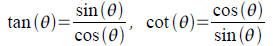
Even-Odd Identities:
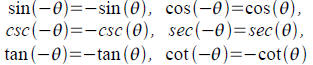
Pythagorean Identities:
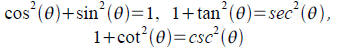
Tool: Verifying trig identities (see p. 441). An
identity is an
equation that should be true for all values of θ . If it is, then
you can use the identities you already know to simplify both
sides to be equal to each other.
Other suggestions include writing in terms of sines and
cosines, combining fractions over a common denominator,
factoring, and combining like terms.
Tool: Disproving false identities takes one single
angle that
shows they don't work. You may have to try more than one if
you try this method.
2 Sum and Difference Angle Identities
Tool: Sum and difference formulas for cosine maybe
proven
using distance formulas on unit circle using x and y
coordinates (see pp. 446-7)
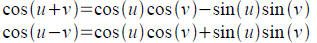
Tool: Cofunction identities by observing that if we
substitute
complementary angles in triangles, we switch our point of
view.
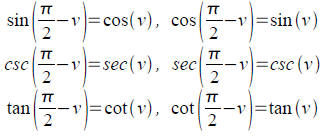
Tool: Sum and difference formulas for sine are
proven by
cofunction identities.
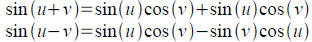
Tool: Addition and Subtraction identities for tangent.
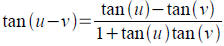
3 Double and Half Angle Identities
Tool: If we set u=v=θ in the sum angle formulas, we
obtain the double angle formulas. Note that double angle
formula for cosine has a couple of equivalent forms based on
the Pythagorean identity.
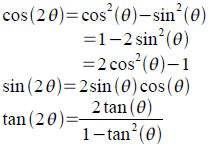
Tool: Half angle identities. These are derived from
the
double angle cosine identities and replacing θ by θ/2
(see p. 462).
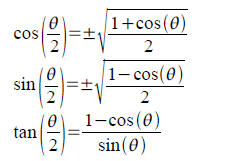
4 Trig Equations
Tool: Trig equations are true only for certain
values of an
angle (unlike identities, which are true for all values).
Always be aware of restrictions. They will tell you where to
look for solutions when you apply inverse trig functions.
Tool: Reference triangles can help you find
multiple
solutions of trig equations.
Tool: Known solutions and 30-60-90, 45-45-90
triangles can
help solve.
Tool: Factoring and finding zeros of factors may
help find
solutions. Think back to when you factored quadratics, but
now we have trig functions.
Tool: Trig identities can be used to solve. You may
have to
factor.
Practice Problems
Simplifying trig expressions:
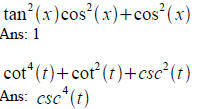
Verifying Trig identities for all angular values:
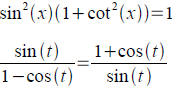
Proving an equation is not an identitiy:
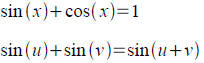
Practice with cosine sum and difference formulas:
Compute the following exactly (no decimal).
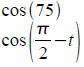
Cofunction identity practice:
Given sin(θ)=1/3
What is sec(90−θ)?
Evaluate the expression exactly (no decimal):
Hint: recognize the proper identity to simplify
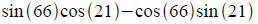
Evaluate the expression exactly (no decimal):
Hint: inverse trig functions output angles. Use triangles
to
find those angles.
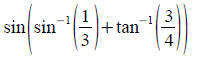
(optional)Practice: You don't really need to
memorize pairs
of sum and difference angle formulas because you can use
even-odd properties to derive one from the other.
Derive the formula for tan(u+v) using even-odd
identities for tangent.
Evaluating trig functions.
Let θ be a first quadrant angle such that tan(θ)= 5/12 .
Compute exactly (no decimal).
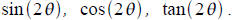
Inverse trig.
Evaluate exactly (no decimal)
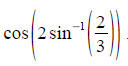
Identity practice.
Show that
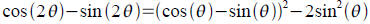
Half angles.
If 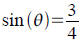 and θ is in first
quadrant, then compute
and θ is in first
quadrant, then compute
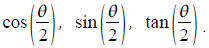
Practice solving equations.
Solve tan(θ)=1 exactly
a) For 0≤θ<90
b) For 0≤θ<360
c) Unrestricted θ
Practice.
Solve sin(θ)=0.9563 to two decimal places for
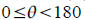
Ans: 73°, 107°
Solve exactly (no decimal).
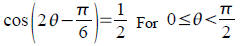
Ans: π/4
Trig factoring.