Number Systems

Integral and Rational Numbers

If we append 0 and the set of additive inverses to the natural numbers, we obtain the set of integers,
Z ={... − 2, −1, 0, 1, 2, ...} = {n ∈ N}∪{0}∪{−n ∈ N} . We denote the set of nonnegative integers
by Z₊ = {0, 1, 2, . . .} = N∪ {0} = {n ∈ Z : n ≥ 0} .

The discreteness of the natural numbers is inherited by the integers:

• If m, n ∈ Z, then m > n implies m ≥ n + 1.
An integer n is even if there is an integer m such that n = 2m. An integer that is not even is odd.

• If n is even if and only if n + 1 and n − 1 are odd.

• If n is even then n² is even, and if n is odd then n² is odd.

Using the properties of N and the order and field properties, we may show that the set of integers
is closed under addition and multiplication.

• For all, n, m ∈ Z, we have n + m ∈ Z, and n · m ∈ Z.

Although addition and multiplication are well defined on the restricted domain Z, it is still not
a field because n^-1 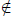Z (unless n = 1). To obtain a field, we must include all of the rational
numbers.

The set of rational numbers, which we denote by Q, consists of all elements of R which may be
written as fractions:

Q ≡ {x ∈ R : x = m/n for m, n ∈ Z, and n ≠ 0}.

• Q is an ordered field and is a subset of any other ordered subfield of R.
· Left as an exercise.

Observe that the fractional representation of any x ∈ Q is not unique since 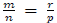whenever
mp = nr. However, for any rational number, we may uniquely choose m and n such that n > 0
and n ≤ p for any p ∈ N and r ∈ Z such that rn = pm (i.e. m and n have no common divisor
greater than 1).

Implications of the Completeness Axiom.

Since Q is an ordered subfield of R, all of the properties of R that depend only on the field and
order axioms are inherited by Q. However, we will show later that certain sequences in Q that
‘virtually’ converge do not have a limit in Q. The completeness axiom (C) ensures that R fills
these gaps and thus distinguishes R from Q.

Archimedean Axiom

• (Axiom of Archimedes) For any x ∈ R, there is an n ∈ Z such that n > x.
· If x ≤ 0, then 1 > x. So suppose x > 0 and define A = {n ∈ N : n ≤ x} . To prove the result it
is sufficient to show that N\A ≠ 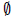. Since A is bounded above by x, the completeness axiom
implies that sup A exists. Then by the definition of sup A, it follows that sup A − 1 is not an
upper bound for A and therefore there is an integer n > sup A − 1. But then n + 1 > sup A,
which implies that n +1 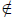A. But then A is not an inductive set and hence N\A ≠ .

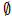The Archimedean axiom can be used to show that Q is a ‘dense’ subset of R.

• For any x ∈ R, there is an n ∈ Z such that n ≤ x < n + 1.
· Let A = {n ∈ N : n > |x|} . Then since the Archimedean axiom implies A is nonempty, the
well-ordering principle implies we may choose n = minA. Therefore n − 1 ≤ |x| < n. For if
n > 1, we have n − 1 ∈ N and therefore n − 1 ≤ |x| , and if n = 1, then n − 1 = 0 ≤ |x| < n.
If |x| = x, then the theorem is proved. If |x| = −x, then 1 − n ≥ x > −n. If x < 1 − n, we
are done. Otherwise, x = 1− n in which case 2 − n > x ≥ 1 − n.

• If x < y, there is a q ∈ Q such that x < q < y.
· Choose N > (y − x)^-1 . Then 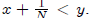Now choose n so that n ≤ 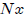< n + 1. Then
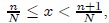which implies

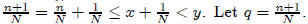
• For any x ∈ R and any ε > 0, there is a q ∈ Q such that |q − x| < ε.
· By the previous result there is a q such that x < q < x + ε. Therefore, 0 < q − x < ε which
implies |q − x| < ε.

• If x ∈ R, then x = sup{q ∈ Q : q < x} .
· Let A = {q ∈ Q : q < x} . Since the Archimedean axiom implies an integer n > −x, it follows
that −n < x, which implies and that A is nonempty. Since it is also bounded above by
x, it follows that sup A exists. Suppose sup A < x. Then there is a rational q such that
sup A < q < x, which implies q ∈ A, but q > sup A, contradicting the definition of sup A.
Similarly if sup A > x, then there is rational q such that x < q < sup A, which implies that q
is an upper bound to A which is less than sup A, again contradicting the definition of A.

Existence of Square Roots

In any ordered field F, the axioms imply that for any y > 0, there is a unique x > 0 such that
x = y². However, the field and order axioms alone do not imply that x > 0 implies a y ∈ F such
that x = y². In fact, this is not true of the rational numbers.

Example: If q² = 2, then 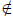q Q.

Suppose q² = 2 for some q ∈ Q. Then, we may choose m, n ∈ Z with no common divisor so
that Then m² = 2n² implies that m² is even and hence m is even. Therefore,
n must be odd (otherwise 2 is a common divisor). But if m is even, then m = 2k for some
integer k,which implies 4k² = 2n². But this implies that 2k² = n², which by the argument
above implies that n is even. A contradiction.

One important implication of the completeness axiom is that the equation 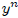= x has a solution
y > 0 for any x > 0 and n ∈ N. Although this follows from results to be established later (i.e. the
intermediate value theorem and the continuity the exponential function), it will be useful to have
the result now for the case where n = 2.

• If x ∈ R₊, then there is a unique y ∈ R₊, such that y² = x, which we denote by 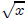and call
the square root of x.
· First observe that since 0 < w < z implies 0² < w² < z², there is at most one y that
satisfies y² = x. If x = 0, then 0 · 0 = 0 implies 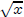= 0. So suppose x > 0 and let
A = { z ∈ R₊₊ : z² < x }. Then for 0 < z < min {1, x} , we have z² < x, and therefore A is
not empty, which implies that y ≡ sup A exists.
· To show that y² = x, suppose first that y² < x. Then wemay choose 0 < z <
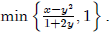
But then (y + z)² = y² +z (2y + z) < y² +z (2y +1) < x, which implies y < y+z ∈ A, which
contradicts y = supA.
· Next suppose y² > x. Then we may choose 0 < z < 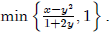But then (y − z)² =
y² − z (2y − z) > y² − z (2y + 1) > x, which implies that y − z is an upper bound of A.
Therefore sup A ≤ y − z < y. A contradiction.

Expansions of the Real Numbers

For any integer b > 1, called the base, let 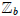≡ {0, ..., b − 1} . A b-expansion in a expression of the
form 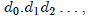where 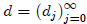is a sequence of integers with 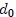∈ Z₊ and 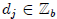for j > 0.
A b-expansion is rational if there is an integer n such that 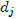= 0 for j ≥ n. A b-expansion that is
not rational is called an irrational b-expansion.

For b = 10, a b-expansion is called a decimal expansion. For b = 2, so that each 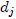∈ {0, 1} ,
it is called a binary expansion, and for b = 3, so that each 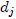∈ {0, 1, 2} , it is called a ternary
expansion.

To assign a real number to each b-expansion 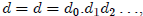let

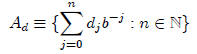
and define

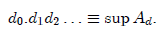
(We show in the Appendix that 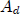is bounded above by 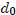+ 1).

• Any rational b-expansion is a rational number. Why?

• Not all irrational expansions are irrational numbers. However, a b-expansion is a rational number
if and only if it eventuallycycles, e.g. .111010101 . . . is a rational number. [Can you state this
precisely and prove it?]

• For any rational number, there is a base b for which it is a rational b-expansion. Why?

• For any base b, any positive real number has a unique irrational b-expansion.
· A proof is provided in the Appendix.

It follows from this theorem that any rational expansion is equal to some irrational expansion. In
fact, one may show that

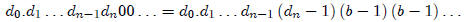
As defined, an expansion can represent only nonnegative numbers. To define expansions for the
negative numbers we define 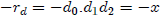  whenever x ≥ 0.