Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

PUTNAM PROBLEM-SOLVING SEMINAR WEEK 5: INEQUALITIES

The Rules. These are way too many problems to consider. Just pick a few problems you
like and play around with them. You are not allowed to try a problem that you already
know how to solve. Otherwise, work on the problems you want to work on.

The Hints. Work in groups. Try small cases. Do examples. Look for patterns. Use lots
of paper. Talk it over. Choose effective notation. Try the problem with different numbers.
Work backwards. Argue by contradiction. Eat pizza. Modify the problem. Generalize.
Don’t give up after five minutes. Don’t be afraid of a little algebra. Sleep on it if need be.
Ask.

Things to remember. Sums of squares are non-negative. The arithmetic mean-geometric
mean inequality (AM-GM): 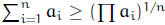(Qai)1/n if the 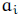are non-negative. The triangle
inequality (the shortest distance between two points is a straight line). Cauchy’s inequality
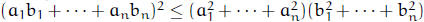. Lagrange multipliers.

1. (a) Find, without using calculus, the minimum surface area of a rectangular box which
holds volume V. (Mark Lucianovic)
(b) Find, without using calculus, the minimum area of an open box — with no top —
which holds volume V.

2. Determine themaximumvalue of (sinA₁)(sinA₂) · · · (sinA_n) given that (tanA₁)(tanA₂) · · · (tanA_n) =
1. (Hint: don’t use calculus without thinking!) (Mark Lucianovic) [We discovered that this
is hard for a # 2!]

3. Given a, b, c nonnegative real numbers such that (a + 1)(b + 1)(c + 1) ≤ 8. Prove that
abc ≤ 1. (Mark Lucianovic)
4. If 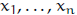are positive real numberswhose product is 1, show that .
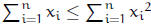(Soren Galatius)

5. The polynomial 4x⁴ − ax³ + bx² − cx + 5 has four positive (real) roots such that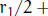
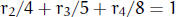. Find them. (Mark Lucianovic)

6. Suppose a, b, c are positive real numbers. Prove that

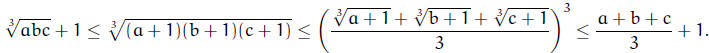
(Soren Galatius)

7. Suppose are positive real numbers. Prove that

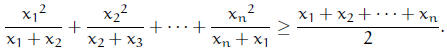
Hint: Don’t be afraid to introduce square roots. (Soren Galatius)

8. (A number-theoretic inequality) Given integers 0 < a < b < c < d < e, prove that
1/ lcm(a, b) + 1/ lcm(b, c) + 1/ lcm(c, d) + 1/ lcm(d, e) ≤15/16. Generalize to integers
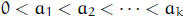. (Mark Lucianovic)

9. (The Power Mean inequality) Suppose 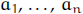are positive real numbers. Define the
kth power mean as

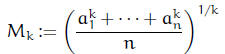
if k ≠ 0, and 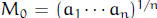. Show that if a > b, then 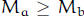, with equality if
and only if all the 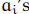are equal. (This can be very handy! If k = 1, we get the arithmetic
mean; if k = 0 we get the geometric mean; if k = −1 we get the harmonic mean; if k = 2 we
get the quadratic mean.)

10. Prove the “logarithmic mean” inequality for a > b > 0:

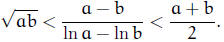
(Mark Lucianovic)

11. Suppose f(x) is a continuous function [a, b] → 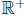(a < b). Figure out what the
integral version of the arithmetic mean should be (see the Power Mean statement above).
State the integral version of the quadratic mean-arithmetic mean inequality. Prove it!

Home