Greatest Common Factor and Least Common Multiple

Review of Basic Concepts and Facts:

(1) The greatest common factor (gcf) of two or more numbers is the greatest number that divides these
numbers.

Example.
12 has factors: 1, 2, 3, 4, 6, 12;
18 has factors: 1, 2, 3, 6, 9, 18;
12 and 18 have common factors: 1, 2, 3, 6.
Hence, the greatest common factor is 6. we use gcf(12, 18) denote the greatest common factor. Thus,
gcf(12, 18) = 6

Example. Find the greatest common factor of 12, 18, 24.

(2) The least common multiple (lcm) of two or more numbers is the smallest number that is a multiple of
these numbers.

Example.
12 has multiples: 12, 24, 36, 48, 60, 72, 84, …;
18 has multiples: 18, 36, 54, 72, 90, …;
12 and 18 have common multiples: 36, 72, ….;
Hence, the least common multiple is 36. We denote the least common multiple by lcm(12, 18) = 36.
Two numbers are relatively prime if their greatest common factor is 1.

Example. 11 and 20.
Problem 1. Find the greatest common factor of 30, 60, 75.
Problem 2. Find the greatest common factor of 120, 180, 300.
Problem 3. Find the least common multiple of 3, 10, 5.
Problem 4. Find the greatest common factor of 2322 and 654.

Euclid's algorithm
Given two numbers not prime to one another, to find their greatest common factor.
The algorithm is based on the following two observations:
If b|a then gcf(a, b) = b.
If a = bn + r, for whole numbers n and r, then gcf(a, b) = gcf(b, r).

Indeed, every common divisor of a and b also divides r. Thus gcf(a, b) divides r. But, of course,
gcf(a, b)|b. Therefore, gcf(a, b) is a common divisor of b and r and hence gcf(a, b) = gcf(b, r). The reverse is
also true because every divisor of b and r also divides a.

Solution:

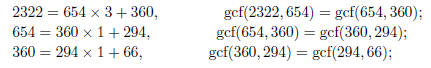
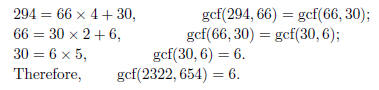
Problem 5. Find the gcf(2703, 1113)
Problem 6. Find the greatest common factor of 1008, 1260, 882, 1134
Problem 7. There is a whole number n such that gcf(n, 28) = 4 and lcm(n, 28) = 252. what is n?.

Relationship between gcf(a, b) and lcm(a, b)
gcf(a; b) × lcm(a, b) = a × b:

Problem 8. Find lcm(21672, 11352).

BYU Math Circle
Homework (Lesson 3)

(1) Number a is one third of number b. The greatest common factor of a and b is 54. What are a and b?

(2) The product of two numbers is 5766 and their greatest common factor is 31. What are these numbers?

(3) Find five consecutive whole numbers such that their product is 55440.

(4) A old couple has three children who live in different towns. The oldest child visits their parents once
per every 6 days, the second oldest child visits their parents once per every 8 days, and the youngest
child visits their parents once per every 12 days. They accidently have a family reunion on October 1.
When is the next reunion?

(5) Find the smallest counting number a such that a x 338 is a square number.

(6) There are numbers of balls with the same weight in a box. Each ball is more than one pound. The total
weight of all balls is 201 pounds. After taking out a number of balls, the weight of the balls in the box
is 183 pounds. What is the weight of each ball?

A Challenge Problem

(8) There are certain things whose number is unknown. Repeatedly divided by 3, the remainder is 2; by 5
the remainder is 3; and by 7 the remainder is 2. What will be the number?

(9) An old woman goes to market and a horse steps on her basket and crashes the eggs. The rider offers  to
pay for the damages and asks her how many eggs she had brought. She does not remember the exact
number, but when she had taken them out two at a time, there was one egg left. The same happened
when she picked them out three, four, five, and six at a time, but when she took them seven at a time
they came out even. What is the smallest number of eggs she could have had?