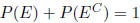Math 141 Concepts to Know #2
• 3.1 - Graphing Inequalities
Graphing Lines
Labeling lines (EQUALITIES!)
Shading the FALSE region
Finding corner points
Bounded - can enclose feasible region in a circle
Unbounded - cannot enclose feasible region in a
circle
• 3.2 - Setting-up LP Problems
Defining variables correctly
OBJ Function (Max or Min statement)
Constraints (Almost always inequalities)
• 3.3 - Graphical Solutions to LP Problems
Graph constraints to find feasible region -
including corner points
Look at the placement of the feasible region -
decide if a max or min exists in that region
Set up chart with corner points and evaluate OBJ
function at each corner point
Locate the max or min value depending on the
problem
If solving a word problem, be able to give answer
in terms the problem. Be able to determine
leftover resources.
• 6.1 - Sets and Set Operations
Know how to read both roster and set-builder no-
tation
Know the meaning of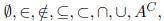 
and U
Know DeMorgan’s Laws
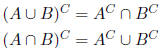
Be able to shade portions of Venn diagrams
Be able to use set notation to describe regions
Be able to read set notation to describe sets in
words
• 6.2 - The Number of Elements in a Set
n(A) = the number of elements in a set
If disjoint, n(A ∪ B) = n(A) + n(B)
For any sets, n(A ∪ B) = n(A)+n(B)−n(A∩B)
Be able to fill in the sections of a Venn diagram
with the number of elements in each section
• 6.3 - The Multiplication Principle
he total # of ways to perform a large task is
the product of the # of ways to perform each
subtask
Be able to draw a tree diagram
• 6.4 - Permutations and Combinations
Permutations - ORDER MATTERS!
Things in a Line or Row, Titles for Group
Members, etc.
n! ways to permute n distinct objects
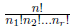ways to permute n non-distinct obj.
Combinations - ORDER DOES NOT MATTER!
Groups where people have no titles, etc.
Know how to use calc. to find the # of perm. and
comb.
Mixed Problems - counting with both perm. and
comb. in the same problem
• Counting Handouts
• 7.1 - Experiments, Sample Spaces, and
Events
Sample Points - outcomes of an exp.
Sample Space (S) - all possible sample points
A common sample space is that of rolling two
fair dice.
Events - subsets of S
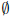- impossible event
S - certain event
Simple Events - contain exactly one sample
point
There are 2n total events for an exp. having
n sample points.
Mutually Exclusive Events - don’t occur at the
same time
A ∩ B =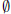 
P(A ∪ B) = P(A) + P(B)
• 7.2 - Definition of Probability
P(E) denotes the prob. that event E occurs
P(E) is a NUMBER such that 0 ≤ P(E) ≤ 1
Uniform Sample Space - all outcomes are equally
likely; the prob. of each simple event is 1/n
where n=the number of outcomes
Probability Distribution - a TABLE giving the
prob. associated with each simple event
• 7.3 - Rules of Probability
P(S) = 1
0 ≤ P(E) ≤ 1 for every event E
P(E ∪ F) = P(E) + P(F) − P(E ∩ F)
