Introduction to Linear Models

Solutions to systems of linear equations

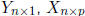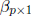Consider the equation Y = Xβ where and . For
a given X and Y (observed data), does there exist a solution β to
this equation?

If p = n (i.e. X square) and X is nonsingular, then yes and
the unique solution is 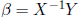. Note that in this case, the
number of parameters is equal to the number of subjects, and
we could not make inference.

Suppose p ≤ n and Y ∈ C(X), then yes though the solution
is not necessarily unique. In this case, 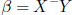is a solution
since 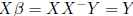for all Y ∈ C(X) by Definition of
generalized inverse. Consider following 2 cases:

If r(X) = p, (X full rank) then the columns of X form a basis
for C(X) and the coordinates of Y relative to that basis are
unique (recall notes section 2.2) and therefore the solution β
is unique.

Suppose r(X) < p. If β* is a solution to Y = Xβ then
β* + w, w ∈ N(X) is also a solution. So we have the set of
all solutions to the equation equal to
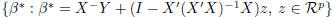. Note
that 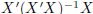is the orthogonal projection operator onto
C(X') and so 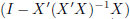is the orthogonal
projection operator onto .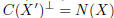

In general, Y ≠ C(X) and no solution exists. In this case, we
look for a vector in C(X) that is "closest" to Y and solve the
equation with this vector in place of Y . This is given by MY
where 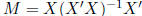is the orthogonal projection
operator onto X. Now solve:

MY = X β

The general solution (for r(X) ≤ p) is given by
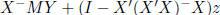and again there are infinite
solutions. Let the SVD of X be given by 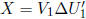. We
know the MP generalized inverse of X is .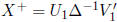
Therefore,

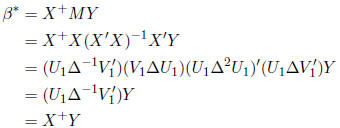
So the general solution is given by

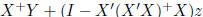
Now assume r(X) = p. In this case, we have
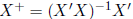and so

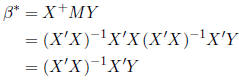
Random vectors and matrices

Definition: Let 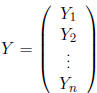be a random vector with
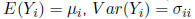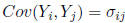and . The
expectation of Y is given by

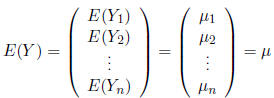
Similarly, the expectation of a matrix is the matrix of expectations
of the elements of that matrix.

Definition: Suppose Y is an n ×1 vector of random variables.
The covariance of Y is given by the matrix:

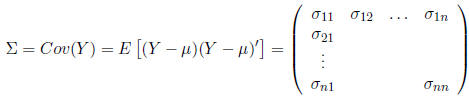
where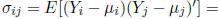

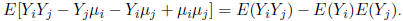
Theorem: Suppose Y is a random n ×1 vector with mean
E(Y ) = μ and covariance 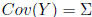. Further suppose the
elements of 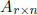and 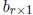are scalar constants. Then,



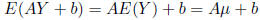
and

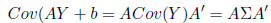
Definition: Let and be random vectors with
E(Y ) = μ and E(W) =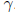 . The covariance between Y and W is
given by



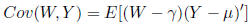
We call this a matrix of covariances (not necessarily square) which
is distinct from a covarince matrix.

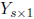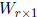Theorem: Let and be random vectors with
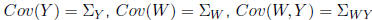and
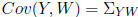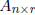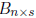. Further suppose and are
matrices of constant scalars. Then

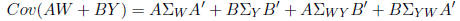
Theorem: Covariance matrices are always positive semi-definite.
Proof: Let 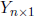be a random vector and

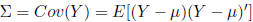where μ= E(Y ). We need
to show that for any 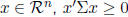. Let Z = (Y -μ ), then
we have:

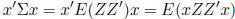	(since x is a vector of scalars)
	(where w = Z'x)

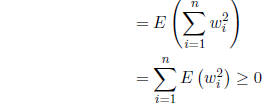Since the expectation of a non-negative random variable will
always be non-negative. Note that if w_i = 0 for all i, then we have
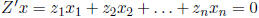where z_i is the ith column of
Z'. This implies dependency among the columns and singularity of
the covariance matrix.