Intermediate Algebra
Course Description: This course is designed to prepare the student for
college algebra. It
covers first-degree equations and inequalities, linear functions, systems of
linear equations,
polynomials, factorization, rational expressions, negative and rational
exponents, radicals,
quadratic equations, graphing functions, logarithms, and application problems.
Prerequisite: MATH 025/010 with C grade or higher, or Math Placement
Test (COMPASS
Algebra score of 41 or higher).
Textbook and Supplies:
• Intermediate Algebra , 4th edition (Student Support Edition), by
Larson/Hostetler,
published by Houghton/Mifflin
• Scientific calculator (No graphing calculators!)
• Regular paper and graph paper
Course Objective: Students who complete Math 108,
Intermediate Algebra, will have a strong
understanding of the topics listed in the course description and in the detailed
list of course
outcomes. This course will prepare students for Math 130, Math 143, Math 147 and
other
courses which have an Intermediate Algebra pre-requisite.
Outcomes Assessment: Daily assignments, exams, and
a comprehensive final exam will be
used to assess how well students achieve the expected course outcomes. Exams as
well as
student evaluations will be analyzed to help improve curriculum and instruction
for the course.
Also, regular informal feedback will be solicited in an effort to improve the
class as it progresses.
The course content includes:
a. Rational numbers (addition, subtraction, multiplication, and division)
b. Variable expressions (simplify, translate, evaluate)
c. Operations on sets of numbers (union, intersection)
d. Set-builder notation and interval notation
e. First degree equations in one variable (solve, translate from application
problems such as percent
problems, mixture problems, business related problems, uniform motion problems,
investment problems)
f. First degree inequalities (solve and graph simple, compound)
g. Linear functions (evaluate, graph, find slope)
h. Find length and midpoint of a segment
i. Write the equations for lines (including parallel lines and perpendicular
lines)
j. Solve systems of linear equations (use graphs, substitution method, addition
method)
k. Polynomials (add, subtract, multiply, divide using long division and
synthetic division, evaluate, factor)
l. Solve polynomial equations by factoring
m. Simplify exponential expressions having integer and variable exponents
n. Scientific notation
o. Expressions with rational exponents (simplify, change to radical form)
p. Radical expressions (simplify, add, subtract, multiply, divide)
q. Complex numbers (simplify, add, subtract, multiply, divide)
r. Solve equations containing radicals
s. Functions (domain, range, graph, use vertical line test, add, subtract,
multiply, divide, find inverse, do
composition of functions)
t. Rational expressions (find the domain, simplify, multiply, divide, add,
subtract, simplify complex
fractions)
u. Solve rational equations (including application problems like work problems,
uniform motion
problems, proportions, variations, and literal equations)
v. Solve quadratic equations (use factoring, completing the square, and
quadratic formula)
w. Solve equations that are quadratic in form
x. Solve quadratic and rational inequalities
y. Parabolas (find axis of symmetry, vertex, x-intercepts, graph)
z. Exponential functions (evaluate, graph)
aa. Logarithms (log notation, properties of logarithms, evaluate logs with and
without a calculator, solve
log equations, graph log functions using ordered pairs)
These additional, optional topics may be covered by some
instructors:
a. Absolute value equations
b. Absolute value inequalities
c. Evaluate determinants (2 x 2 and 3 x 3)
d. Solve a system of equations using Cramer’s Rule
e. Solve a system of equations using gaussian elimination with matrices
f. Application problems with systems of equations
g. Application problems with quadratic equations and functions
h. Application problems with exponential equations and functions
i. Application problems with logarithmic equations and functions
As part of departmental analysis of outcomes in this
course and its place in the Mathematics
program, student completion of the pre-requisite, success in the current course,
success in
subsequent courses and student satisfaction will be reviewed by the instructor
and the department
chair. A report containing this information will be submitted by department
On-line Course Evaluation: Students are strongly
encouraged to complete evaluations at the
end of the course. Evaluations are very important to assist the teaching staff
to continually
improve the course. Evaluations open up two weeks prior to the end of the
course.
The last day to complete an evaluation is the last day of the course.
During the time the evaluations are open, students can complete the
course evaluations at their convenience from any computer with Internet access,
including in the
open lab in the Library and in the SUB. When students log in they should see the
evaluations for
the courses in which they are enrolled. Evaluations are anonymous. Filling out
the evaluation
should only take a few minutes. Your honest feedback is greatly appreciated.
Policies and Procedures:
• EXAMS: Regular exams will be given at the Campus Testing
Center. The Twin Falls
Center is located in the Meyerhoeffer Building, Room 230 and is open Monday
through
Thursday, 8:00 am – 9:30 pm; and Friday, 8:00am – 5:00 pm. You must have a photo
ID
and arrive at least one hour before closing times. The exams will be available
over a 3-
day period beginning the day we review the test material in class. There will be
no makeup
exams given! If you have an unforeseeable and unavoidable emergency, I will
replace
that exam score with the final exam score, weighted to 100 points. The
comprehensive,
common final exam will be given in the classroom on the Twin Falls campus with
the
instructor present. A make-up final will not be granted under any circumstances.
• HOMEWORK: Homework will be assigned during most class
sessions and will be due
at the beginning of the next class session. Late homework will not be accepted
under any
circumstances! At the end of the semester, the 4 lowest homework scores will be
dropped. Each page of each homework assignment must have your name, class time
(ex
8:00 am), and exercise section number. You must show your work to receive full
credit!
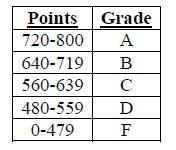
• GRADING:
| 5 Exams worth 100 points each | 500 points |
| Homework | 100 points |
| Final Exam | 200 points |
| Total Possible | 800 points |
• CHEATING: Cheating is unacceptable. Students caught
cheating will be given a 0% for
that assignment or exam and may face further disciplinary action.
• ATTENDANCE: As dictated by CSI policy, when the number
of class hours absent
exceeds twice the number of course credits (4 classes for this course), the
instructor will
drop the student from the course. A class missed due to required participation
in a
verified school activity will not be considered an absence. All students are
responsible
for everything presented in class whether they are there or not.
• COMMUNICATION: Email is the primary source of written
communication with all
CSI students. Messages from instructors and various offices such as Admission
and
Records, Advising, Financial Aid, Scholarships, etc. will be sent to the
students’ CSI
accounts (NOT their personal email accounts). It is the student’s responsibility
to check
their CSI email accounts regularly. Failing to do so will result in missing
important
messages and deadlines.
• STUDENT BEHAVIOUR: Refer to pages 14-16 in the CSI catalog.
• LEARNING ASSISTANCE RESOURCES:
a. Instructor: If you need extra explanation, stop by my office during
office hours or set up an appointment for help at another time.
b. Textbook: Read and study the examples in your textbook.
c. Free Peer Tutoring: Free tutoring is available at the Math Lab (Shields
207) and
the Academic Development Center Instruction Lab (GRM 202).
d. DVDs and CDs: DVDs and CDs of the subject matter are available in
several locations.
i. CSI Library – Front Desk (overnight checkout or view at the Library)
ii. All CSI Outreach Centers (overnight checkout)
e. Study Groups: Study groups are a great way to learn. Organize one right
away!
• COMPUTER LITERACY: Please refer to the College of
Southern Idaho Catalog, under
Computer Literacy in the section, “Degree and Certificate Requirements” on page
25 of
the College of Southern Idaho 2007-2008 Catalog.
• STUDENTS WITH DISABILITIES: Any student with a
documented disability may be
eligible for related accommodations. To determine eligibility and secure
services,
students should contact the coordinator of Disability Services at their first
opportunity
after registration for a class. Appointments may be made or more information is
available at (208)732-6254 (voice) or (208)734-9929 (TDD).
Course Outline
(Tentative and subject to change at any time)
| Date | Section | Topic | |
| August | 28 | Intro, 1.1- 1.3 |
The Real Number System, Operations with Real
Numbers, Properties of Real Numbers |
| 30 | 1.4,1.5, 2.1 |
Algebraic Expressions, Constructing Algebraic
Expressions, Linear Equations |
|
| September | 4 | 2.2, 2.3 | Linear Equations and Problem Solving, Business
and Scientific Problems |
| 6 | 2.3, 2.4 | Business and Scientific Problems, Linear Inequalities | |
| 11 | 2.5, Review |
Absolute Value Equations and Inequalities | |
| Sept 11, 12, 13 – Take Exam 1 in Testing Center | |||
| 13 | 3.1,3.2 | The Rectangular Coordinate System, Graphs of Equations | |
| 18 | 3.3,3.4 | Slope and Graphs of Linear Equations, Equations of Lines | |
| 20 | 3.6,4.1 | Relations and Functions, Systems of Equations | |
| 25 | 4.1,4.2 | Systems of Equations, Linear Systems in Two Variables | |
| 27 | 4.3 | Linear Systems in Three Variables | |
| October | 2 | Review, 5.1 |
Integer Exponents and Scientific Notation |
| Oct 2, 3, 4 – Take Exam 2 in Testing Center | |||
| 4 | 5.2,5.3 | Adding and Subtracting Polynomials, Multiplying Polynomials | |
| 9 | 5.4 | Factoring by Grouping and Special Forms | |
| 11 | 5.5 | Factoring Trinomials | |
| 16 | 5.6 Review | Solving Polynomial Equations by Factoring | |
| Oct 16, 17, 18 – Take Exam 3 in Testing Center | |||
| 18 | 6.1,6.2 | Rational Expressions and Functions, Multiplying
and Dividing Rational Expressions |
|
| 23 | 6.3,6.4 | Adding and Subtracting Rational Expressions,
Complex Fractions |
|
| 25 | 6.5,6.6 | Dividing Polynomials and Synthetic Division,
Solving Rational Equations |
|
| 30 | 6.7, Review |
Applications and Variation | |
| Oct 30, 31, Nov 1 – Take Exam 4 in Testing Center | |||
| November | 1 | 7.1,7.2 | Radicals and Radical Exponents, Simplifying
Radical Expressions |
| 6 | 7.3,7.4 | Adding and Subtracting Radical Expressions,
Multiplying and Dividing Radical Expressions |
|
| 8 | 7.5,7.6 | Radical Equations and Applications, Complex Numbers | |
| 13 | 8.1,8.2 | Solving Quadratic Equations: Factoring and
Special Forms, Completing the Square |
|
| 15 | 8.3,8.4 | The Quadratic Formula, Graphs of Quadratic Functions | |
| 20 | 8.5,8.6 | Applications of Quadratic Functions, Quadratic
and Rational Inequalities |
|
| 22 | Thanksgiving Vacation – No class! | ||
| 27 | Review | ||
| Nov 27, 28, 29 – Take Exam 5 in Testing Center | |||
| 29 | 9.1,9.2 | Exponential Functions, Composite and Inverse Functions | |
| December | 4 | 9.2,9.3 | Composite and Inverse Functions, Logarithmic Functions |
| 6 | 9.4,9.5 | Properties of Logarithms, Solving Exponential and
Logarithmic Equations |
|
| 11 | 9.6, Review |
Applications | |
| 13 | Review | ||
Final Exam – Monday, December 17, 4:00 pm to 6:00 pm
Twin Falls Campus, room to be announced


