Linear Equations. Slope, Intercepts, Applications
•Linear Equations in two variables
•Slope of a line
•Intercepts
•y = mx+b
•Applications
x- and y-intercepts of an equation.
Definition In the graph of any equation of two variables, the
points where the graph of an equation crosses the x-axis are
called the x-intercepts and the points where the graph crosses
the y-axis are called the y-intercepts
What do the coordinates of an x-intercept look like?
To find them set = 0 and solve for .
What do the coordinates of a y-intercept look like?
To find them set = 0 and solve for .
The intercepts of a linear equation are easier to locate than the
intercepts of most other equations.
x- and y-intercepts of a linear equation.
Find the x- and y- intercepts for 4x - 3y = 12.
Find the x- and y-intercepts for 7x - .2y = 12.
Could a linear equation have more than one x-intecept?
Intercepts for the Price-demand equation.
d = 1720 - .50p
What are the p- and d-intercepts? What do they mean here?
The slope of a linear equation. the price-demand
equation
d = 1720 - .50p
If price increases by $1 how much does demand decrease?
Does this depend on the starting price?
If price increases by $1000 how much does demand decrease?
Does this depend on the starting price?
Is the decrease in demand always .50 times the increase in price?
Slope-Intercept form (y = mx+b).
Definition An equation of the form
y = mx+b
is a linear equation in slope-intercept form.
Put 4x - 3y = 12 into slope-intercept form.
What are m and b?
Give a verbal description of m and b.
Price-demand equation. d = 1720 - .50p.
Put this into slope-intercept form.
What are m and b?
What is the meaning of m? of b?
Application. Depreciation.
Linear Depreciation. Office equipment was purchased for $20,000
and is assumed to have a scrap value of $2,000 after 10 years. If
its value is depreciated linearly (for tax purposes) from $20,000
to $2,000.
1. What is the slope of the line? Write a verbal interpretation
of the slope of the line.
2. Find the linear equation that relates value (V) in dollars to
time (t) in years. (Hint. you know two points.)
Linear Depreciation. Office equipment was purchased for
$20,000
and is assumed to have a scrap value of $2,000 after 10 years. If
its value is depreciated linearly (for tax purposes) from $20,000
to $2,000:
1. What would be the value of the equipment after 6 years?
2. Graph the equation 
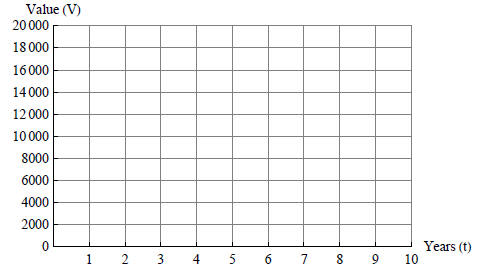
Application. Linear Interpolation
The price of a cup of coffee in a coffee bar depends on the size of
the cup. The 8-ounce cup costs $2.10, but the larger 20-ounce
cup costs $3.30. Without any other information, how could you
estimate the cost of a 10-ounce cup, or a 16-ounce cup?
Sometimes business people use a method known as linear
interpolation.
This means that they assume that the price p of a
cup of coffee and the size q of the cup obey a linear equation.
So the graph of the linear equation is a line and we know two
points on this line. (q, p) = (8, 2.10), (20, 3.30).
Application. Linear Interpolation
two points on the line. (q, p) = (8, 2.10), (20, 3.30).
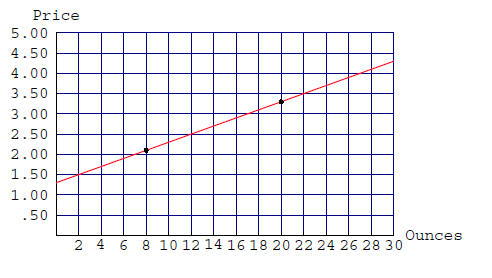
Slope.
Point-slope form. p - 2.10 = .10(q - 8)
Slope-intercept form. p = .10q +1.30.
Application. Linear Interpolation
Slope-intercept form. p = .10q +1.30.
Use linear interpolation to find the price of a 12-ounce cup of
coffee.
Give a verbal interpretation for the slope.
If the size of the cup increases by 4 ounces, by how much does
the cost increase?
Give a verbal interpretation for the y-intercept.
Application. So Relax
West field shopping mall has an accupressure massage station
called "So Relax." Here is the pricing structure.
10 minutes $13.00
15 minutes $19.00
20 minutes $26.00
•Plot these prices
•Is the price a linear function
of the time in minutes?
•What is the best deal?



