Linear Equations and Matrices
Definition 1. A system of m linear equations in n unknowns is a
set of m linear equations each in n unknowns of
the form:
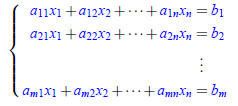
where
• x1,x2, . . . ,xn are n unknowns.
• The aij and bi are the the given constants
A solution to the linear system (1) is a sequence of n numbers s1,
s2, . . . , sn such that (1) is satisfied when x1
=
s1,x2 = s2, . . . ,xn = sn.
Example 1. Determine if the following systems are linear and check if the given s1, s2, . . . are their solutions
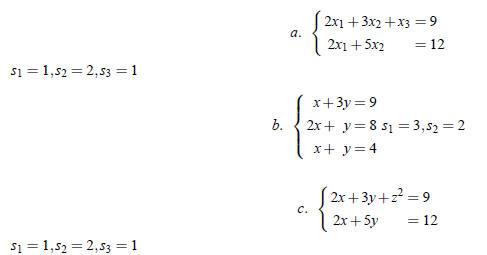
Definition 2.
• We say that the linear system We say that two linear systems are equivalent
if they both have exactly the same
solutions. is consistent if it has a solution. Otherwise it is called
inconsistent.
• When b1 = b2 = · · · = bm = 0, we say that
(1) is a homogeneous system. Note that a homogeneous system
always admits the solution x1 = x2 = · · · = xm
= 0, called the trivial solution. A solution to a homogeneous
system where not all of x1,x2, . . . ,xm are
zero is called a nontrivial solution.
Equivalent linear systems and properties. We say that two linear
systems are equivalent if they both have exactly
the same solutions.
Properties.
The system (1) is equivalent to a new linear system manipulated by:
1. Interchanging the ith and the jth equations
2. Multiplying an equation by a nonzero constant
3. Replacing ith equation by c times the jth equation plus the ith equation, i≠j.
That is, replacing
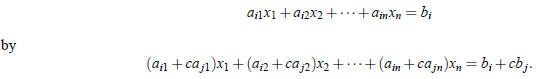
Example 2. Consider the system
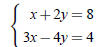
with the solution x = 4,y = 2. Check that the following systems also have the same solution
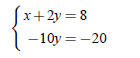
Note: (2b)2 (2a)2−3(2a)1
(2a)2−3(2a)1
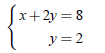
Note: (2c)2 (-1/10)(2b)2
(-1/10)(2b)2
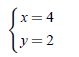
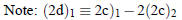
Solving linear systems - Method of elimination. To
find a solution to a linear system, we use the method of
elimination; that is, we eliminate some variables by using the properties 1,2,3
above to get to simpler linear systems,
easier to solve.
Example 3. 2, 6/p8, 16/p9.


