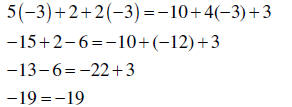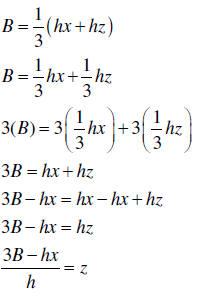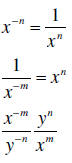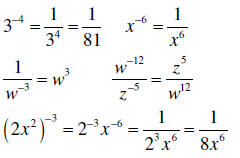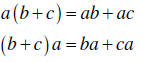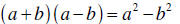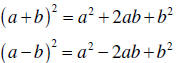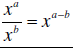SAMPLE PLACEMENT TEST FOR MATHEMATICS
Sample Questions for Arithmetic Skills
1. Estimate to the nearest hundred: 31,253−1275
2. Round to the nearest hundredth: 6.4562
3. Find the missing number:
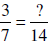
4. Write as a mixed number
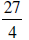
5. Combine:
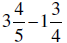
6. Divide:
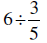
7. Combine: 1.3 + 1.8 + 2.6 + 7.2 + 0.8
8. Multiply: 0.002× 4.31
9. Divide: 3.186 ÷ 0.03
10. Mr. Carr is installing wall-to-wall carpeting in a room that measures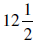 ft.
by 9 ft. How much will it
ft.
by 9 ft. How much will it
cost Mr. Carr if he purchases carpet priced at $26.00 per square yard?
11. Write as a percentage: 3/8
12. Find 250% of 36
13. In a given university, 720 of the 960 new students will study algebra
during their first year. What
percentage of the new students will study algebra during their first year?
14. An investment pays 8% simple interest per year. If the investment earns
$84 interest in the first year,
then how much money was originally invested?
15. If Mary wants to finish a 16 kilometer race in no more that 2 hours, then
what is the minimum
distance in kilometers that she should run every 15 minutes?
Answers For Sample Arithmetic Questions
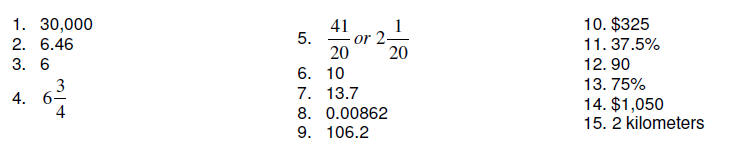
Sample Questions for Elementary Algebra Skills
1. Combine Like terms: 13a −15b − a + 2b
2. Multiply: (2x −1)(4x +1)
3. Solve for x: 5(2x − 3) − (x + 3) = 0
4. Find all the factors of
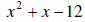
5. Factor out the greatest common factor:
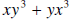
6. Divide:
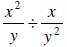
7. Simplify:
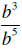
8. Multiply:
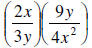
9. Simplify:
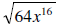
10. The average of x, y, and z is 80. If two of the numbers are 74 and 78, then what is the other number?
11. Find all the solutions of 4( x + 3) (3x − 2) = 0
12. Find the value of x in the solution of the following system of equations:
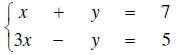
13. In which quadrants (I, II, III, and/or IV) will you find ordered pairs for which x > -3 and y<0?
14. Find the values of x for which − x − 3 >12
15. What are all values of x for which
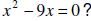
16. Factor:
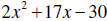
17. Solve:
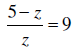
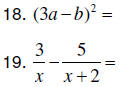
20. If Sam walks 650 meters in x minutes then write an algebraic expression
which represents the number of
minutes it will take Sam to walk 1500 meters at the same average rate.
Answers For Sample Elementary Algebra Questions
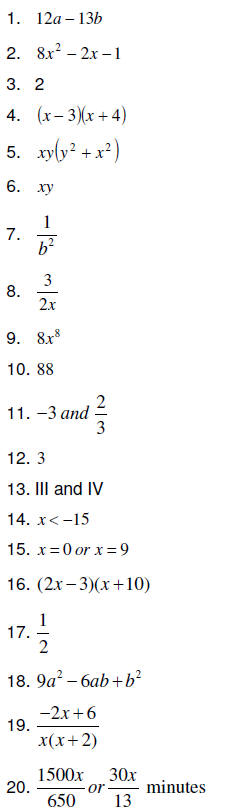
Sample Questions for College Level Mathematics
1. Simplify each fraction:

2. Combine the following polynomial:
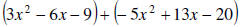
3. Express with positive exponents:
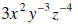
4. Today’s fastest modem computers can perform one operation in 1 x 10-8
second. How many operations
can such a computer perform in 1 minute? Answer in scientific notation.
5. Remove the greatest common factor:
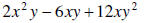
6. Solve for the root(s) of the quadratic equation:
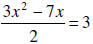
7. Simplify the rational expression:
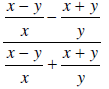
8. Solve and graph on a number line: 4(2 − x)≤3
9. Solve for h: 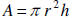
10. Factor: 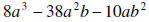
11. Find the slope of the line 4x − 3y − 7 = 0
12. Line p has a slope of
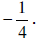 What is the slope of a line parallel to line
p? What is the slope of a line
What is the slope of a line parallel to line
p? What is the slope of a line
perpendicular to line p?
13. Find the equation of a line that passes through (−1, 6) and (2, 3).
14. Find the indicated values for a function: f (x) = 3x − 7
a) f (− 2) b) f (4)
15. To the nearest thousandth, how much error can be
tolerated in the length of a wire that is supposed to be
2.57 centimeters long? Specifications allow an error of no more than 0.25%
Answers for Sample College-Level Mathematics Questions
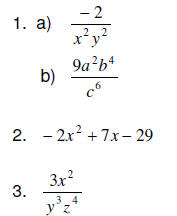
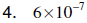 operations in one
minute
operations in one
minute
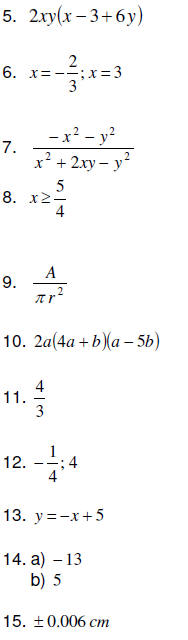
A Brief Review of Math Skills
| Topic | Procedure | Examples |
| Absolute Value | The absolute value of a number is
the distance between that number and zero on the number line. The absolute value of any number will be positive or zero. |
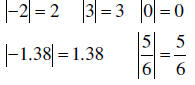 |
| Adding signed numbers with the same sign |
If the signs are the same, add the absolute values of the numbers. Use the common sign in the answer |
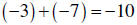 |
| Adding several signed numbers with opposite signs |
If the signs are different: 1. Find the difference of the larger absolute value and the smaller. 2. Give the answer the sign of the number having the larger absolute value. |
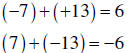 |
| Adding several signed numbers |
When adding several signed numbers, separate them into two groups by common sign, Find the sum of all the positives and all the negatives. Combine these two subtotals by the method described above. |
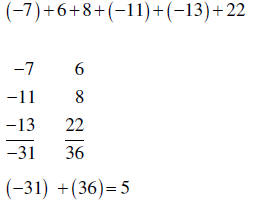 |
| Subtracting signed numbers |
Change the sign of the second number and then add |
(−3) − (−13) = (−3) + (+13) =10 |
| Multiplying and dividing signed numbers |
1. If the two numbers have the same sign, multiply (or divide). The result is always positive. 2. If the two numbers have different signs, multiply (or divide) as indicated. The result is always negative |
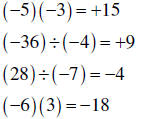 |
| Exponent form | The base tells you what
number is being multiplied. The exponent tells you how many times this number is used as a factor. |
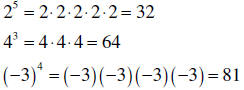 |
| Raising a negative number to a power |
When the base is negative, the
result is positive for even exponents, and negative for odd exponents. |
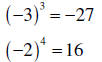 |
| Removing Parentheses |
Use the distributive law to remove parentheses: a(b + c) = ab + ac |
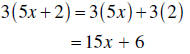 |
| Combining like terms |
Combine terms that have identical letters and exponents |
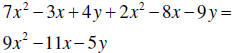 |
| Order of operations | Remember the proper order of operations: 1. Operations inside Parentheses () and brackets [] 2. Exponents 3. Multiplication and Division from left to right. 4. Addition and Subtraction from left to right. |
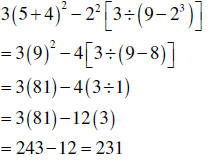 |
| Substituting into variable expressions |
1. Replace each letter by the
numerical value given. 2. Follow the order of operations in evaluating the expression |
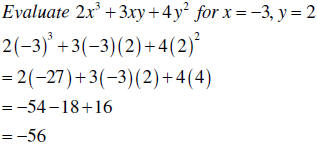 |
| Using formulas | 1. Replace each variable in the formula by the given values. 2. Evaluate the expression. 3. Label units carefully |
Find the area of a circle with radius feet. Use 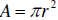 with with
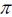 approximatley 3.14. approximatley 3.14.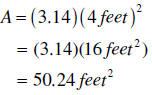 The area of the circleis approximately 50.24 square feet. |
| Removing grouping symbols |
1. Remove innermost grouping symbols first. 2. Continue until all grouping symbols are removed. 3. Combine like elements. |
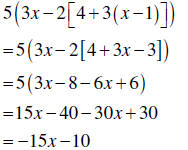 |
| Solving equations without parentheses or fractions |
1. On each side of the equation, collect like terms if possible. 2. Add or subtract terms on both sides of the equation in order to get all terms with the variable on one side of the equation. 3. Add or subtract a value on both sides of the equation to get all terms not containing the variable on the other side of the equation. 4. Divide both sides of the equations by the coefficient of the variable. 5. If possible, simplify solution. 6. Check your solution by substituting the obtained value into the original equation. |
Solve for X: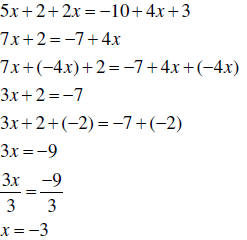 Check:
Is x = −3 a solution |
| Solving equations with parentheses and/or fractions |
1. Remove any parentheses. 2. Simplify, if possible. 3. If fractions exist, multiply all terms on both sides by the lowest common denominator of all the fractions. 4. Now follow the remaining steps of solving an equation without parentheses or fractions. |
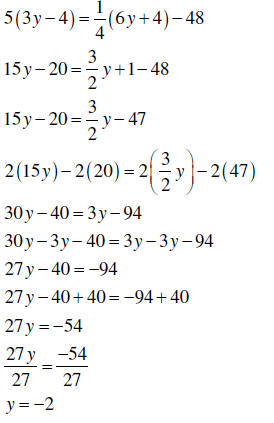 *Remember to check your solution (see previous example) |
| Solving formulas | 1. Remove any parentheses and simplify if possible. 2. If fractions exist, multiply all terms on both sides by the LCD, which may be a variable. 3. Add or subtract terms on both sides of the equation in order to get all terms containing the desired variable on one side of the equation and all other terms on the opposite side of the equation. 4. Divide both sides of the equation by the coefficient of the desired variable. This decision may involve other variables. 5. Simplify, if possible. 6. Check your solution by substituting the obtained expression into the original equation. |
Solve for z:
|
| Solving Inequalities | 1. Follow the steps for solving a
first-degree equation up until the division step. 2. If you divide both sides of the inequality by a positive number, the direction of the inequality is not reversed. 3. If you divide both sides of the inequality by a negative number, the direction of the inequality is reversed. |
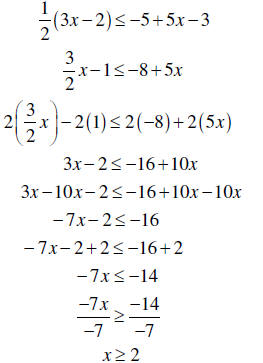 |
| Multiplying monomials |
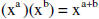
1. Multiply the numerical |
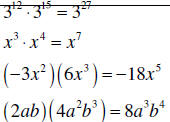 |
| Dividing monomials | 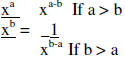
1. Divide or reduce the fraction |
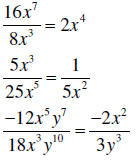 |
| Exponent of zero | 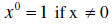 |
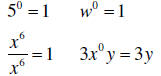 |
| Raising a power to a power |
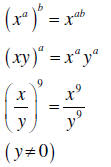
1. Raise the numerical coefficient to |
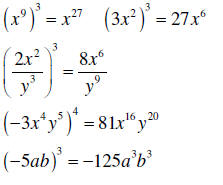 |
| Negative exponents | If x ≠ 0 and y ≠ 0, then
|
Write with positive exponents
|
| Scientific notation | A number is written in scientific notation if it is the form: 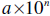 where 1 ≤ a <10 and n is an integer |
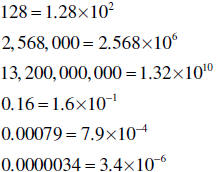 |
| Add polynomials | To add two polynomials, we add the respective like term |
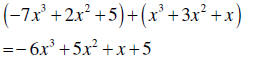 |
| Subtracting polynomials |
To subtract polynomials, change all signs of the second polynomial and add the result to the first polynomial: (a) − (b) = (a) + (−b) |
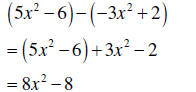 |
| Multiplying a monomial by a polynomials |
Use the distributive property:
|
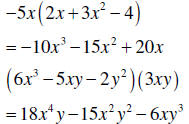 |
| Multiplying two binomials |
1. The product of the sum and difference of the same two values yields the difference of their squares.
2. The square of a binomial yields a
3. Use FOIL for other binomial |
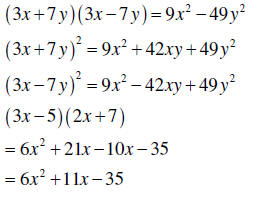 |
| Multiplying two polynomials |
To multiply two polynomials, multiply each term of one by each term of the other. This method is similar to the multiplication of many-digit numbers. |
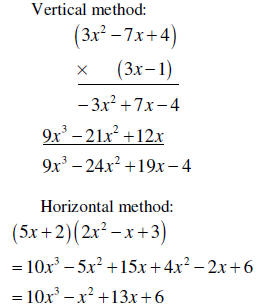 |
| Multiply three or more polynomials |
1. Multiply any two polynomials. 2. Multiply the result by any remaining polynomials. |
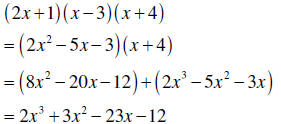 |
| Dividing a polynomial by a monomial |
1. Divide each term of the
polynomial by the monomial. 2. When dividing variables use the property:
|
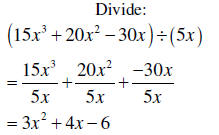 |
| Dividing a polynomial by a binomial |
1. Place the terms of the polynomial and binomial in the descending order. Insert a 0 for any missing term. 2. Divide the first term of the polynomial by the first term of the binomial. 3. Multiply the partial answer by the binomial, and subtract the results from the first two terms of the polynomial. Bring down the next term to obtain a new polynomial. 4. Divide the new polynomial by the binomial using the process described in step 2. 5. Continue dividing, multiplying, and subtracting until the reminder is at a lower power than the variable in the first term of the binomial divisor. |
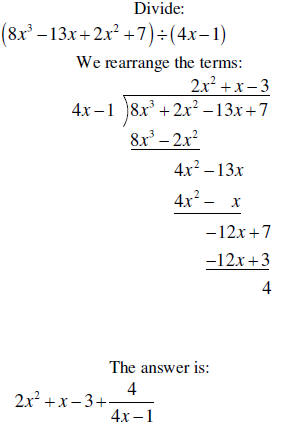 |