Solving Quadratic Equations
22.5 Finding an equation when you know its roots
We have mentioned before that the roots of a quadratic equation are the
solutions or answers
you get from solving the quadatic equation. Working back from the answers, will
take you to an
equation.
 |
Worked Example 110: Find an equation when roots
are given Question: Find an equation with roots 13 and -5 Answer Step 1 : Write down as the product of two brackets The step before giving the solutions would be: (x − 13)(x + 5) = 0 Notice that the signs in the brackets are opposite of the given roots. Step 2 : Remove brackets x2 − 8x − 65 = 0 Of course, there would be other possibilities as well when each term on each side of the equal to sign is multiplied by a constant. |
 |
Worked Example 111: Fraction roots Question: Find an equation with roots 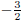 and 4 and 4Answer Step 1 : Product of two brackets Notice that if Therefore the two brackets will be: (2x + 3)(x − 4) = 0 Step 2 : Remove brackets The equation is: 2x2 − 5x − 12 = 0 |
 |
Extension: Theory of Quadratic Equations -
Advanced This section is not in the syllabus, but it gives one a good understanding about some of the solutions of the quadratic equations. |
What is the Discriminant of a Quadratic Equation?
Consider a general quadratic function of the form f(x) = ax2 + bx + c. The
discriminant is defined as:
Δ
= b2 − 4ac.
![]() (22.18)
(22.18)
This is the expression under the square root in the formula for the roots of
this
function. We have already seen that whether the roots exist or not depends on
whether this factor Δ is negative or positive.
The Nature of the Roots
Real Roots ( Δ ≥ 0)
Consider Δ ≥ 0 for some quadratic function f(x) = ax2 +bx+c. In this case there
are solutions to the equation f(x) = 0 given by the formula
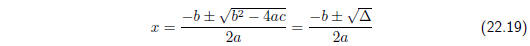
Since the square roots exists (the expression under the
square root is non-negative.)
These are the roots of the function f(x).
There various possibilities are summarised in the figure below.
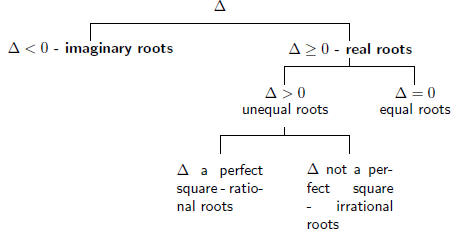
Equal Roots ( Δ = 0)
If Δ = 0, then the roots are equal and, from the formula, these are given by
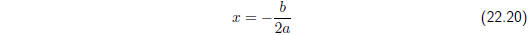
Unequal Roots ( Δ > 0)
There will be 2 unequal roots if Δ > 0. The roots of f(x) are rational
if Δ is a
perfect square (a number which is the square of a rational number), since, in
this
case, 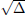 is rational. Otherwise, if Δ is not a perfect square, then the roots are
is rational. Otherwise, if Δ is not a perfect square, then the roots are
irrational.
Imaginary Roots ( Δ < 0)
If Δ < 0, then the solution to f(x) = ax2 + bx + c = 0 contains the square root of
a negative number and therefore there are no real solutions. We therefore say
that
the roots of f(x) are imaginary (the graph of the function f(x) does not
intersect
the x-axis).
|
|
Extension: Theory of Quadratics - advanced exercises |
|
|
Exercise: From past papers |
1. [IEB, Nov. 2001, HG] Given: x2 + bx − 2 + k(x2 + 3x + 2) =
0 (k ≠ −1)
A Show that the discriminant is given by:
Δ = k2 + 6bk + b2 + 8
B If b = 0, discuss the nature of the roots of the equation.
C If b = 2, find the value(s) of k for which the roots are equal.
2. [IEB, Nov. 2002, HG] Show that k2x2 + 2 = kx − x2 has non-real
roots for all real values for k.
3. [IEB, Nov. 2003, HG] The equation x2 + 12x = 3kx2 + 2 has real
roots.
A Find the largest integral value of k.
B Find one rational value of k, for which the above equation has
rational roots.
4. [IEB, Nov. 2003, HG] In the quadratic equation px2 + qx + r = 0,
p, q and r are positive real numbers and form a geometric sequence.
Discuss the nature of the roots.
5. [IEB, Nov. 2004, HG] Consider the equation:
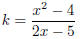 where
where
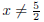
A Find a value of k for which the roots are equal.
B Find an integer k for which the roots of the equation will be
rational and unequal.
6. [IEB, Nov. 2005, HG]
A Prove that the roots of the equation x2 −(a+b)x+ab−p2 = 0
are real for all real values of a, b and p.
B When will the roots of the equation be equal?
7. [IEB, Nov. 2005, HG] If b and c can take on only the values 1, 2 or
3, determine all pairs (b; c) such that x2 +bx+c = 0 has real roots.
22.6 End of Chapter Exercises
1. Solve: x2 − x − 1 = 0 (Give your answer correct to two decimal places.)
2. Solve: 16(x + 1) = x2(x + 1)
3. Solve: 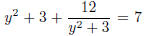 (Hint: Let y2 + 3 = k and solve for k first and use the
(Hint: Let y2 + 3 = k and solve for k first and use the
answer to solve y.)
4. Solve for x: 2x4 − 5x2 − 12 = 0
5. Solve for x:
A x(x − 9) + 14 = 0
B x2 − x = 3 (Show your answer correct to ONE decimal place.)
C 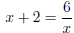
(correct to 2 decimal places)
D 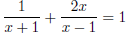
6. Solve for x by completing the square: x2 − px − 4 = 0
7. The equation ax2 + bx + c = 0 has roots
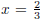 and x = −4. Find one set of possible
and x = −4. Find one set of possible
values for a, b and c.
8. The two roots of the equation 4x2 + px − 9 = 0 differ by 5.
Calculate the value of p.
9. An equation of the form x2 + bx + c = 0 is written on the board. Saskia and
Sven copy
it down incorrectly. Saskia has a mistake in the constant term and obtains the
solutions
-4 and 2. Sven has a mistake in the coefficient of x and obtains the solutions 1
and -15.
Determine the correct equation that was on the board.
10. Bjorn stumbled across the following formula to solve the quadratic equation
ax2+bx+c = 0
in a foreign textbook.
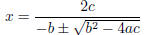
A Use this formula to solve the equation:
2x2 + x − 3 = 0
B Solve the equation again, using factorisation, to see if the formula works for
this
equation.
C Trying to derive this formula to prove that it always works, Bjorn got stuck
along the
way. His attempt his shown below:
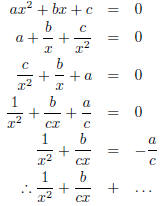 |
|
| Divided by x2 where x ≠ 0 | |
| Rearranged | |
| Divided by c where c ≠ 0 | |
Subtracted 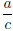 from both sides from both sides |
|
| Got stuck |
Complete his derivation.


