College Algebra

19 The Natural Logarithm

19.1. The irrational number

e = 2.7182818284590451 ...

is most often used as the base for the exponential function. The exponential
function base e is called the natural exponential and the inverse function



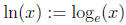
is called the natural logarithm. We shall explain what is natural about
the natural logarithm in two ways.

19.2. First we note that the average rate of change (see Section 14) for the
natural exponential on the interval [x, x + h] is given by

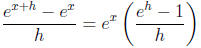
It is proved in calculus that the number e is characterized by the fact that
the ratio 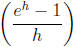is very close to one when h is small. This means that
the average rate of change over a short interval [x, x + h] (the instantaneous
rate of change) is the value e^x of the natural exponential.

Now consider a quantity N governed by an exponential law

N = N₀a^t

and let r = ln(a) be the natural logarithm of the base a. Then a = e^r so
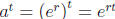and the exponential law takes the form

N = N₀e^rt

Now consider the average rate of change of N over a short time interval
[t, t+ Δt] of duration Δt. Using the above formula with x = rt and h = r Δt
we get

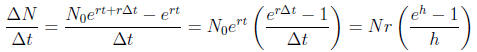
which says that the instantaneous rate of change is Nr. For example, if r =
0.06 this says that the instantaneous rate of change is 6% of N. (Remember:
"per" means divide, "of" means times, and "cent" means 100 so 6 % means
6/100 and 6% of N is 0.06N.) In summary

19.3. The second way of understanding what is natural about the natural
exponential function is to consider a bank account which earns a nominal
interest rate of (say) 6% per year. The interest rate is called nominal because
the actual amount of interest paid depends on how often the bank pays the
interest. An interest rate of 6% per year is the same as an interest rate of
6%/12 = 0.5% per month but if the bank pays the interest every month, the
account will grow by slightly more than 6% in a year. Here is how a few
different banks might pay interest.

(i) The Alaska Bank pays interest compounded annually. This means that
every year it looks at the balance in an account and adds 6%. Thus an initial
deposit of B₀ dollars grows to

B = B₀(1.06)^t

dollars after t years (assuming no other deposits are made during this period).

(ii) The Minnesota Bank pays interest compounded monthly. This means
that every month it looks at the balance in an account and adds 6/12% =
0.5%. Thus an initial deposit of B₀ dollars grows to

B = B₀(1.005)^12t

dollars after 12t months = t years (assuming no other deposits are made
during this period.)

(iii) The Wisconsin Bank pays interest compounded weekly. This means
that every week it looks at the balance in an account and adds 6/52% =
0.001154%. Thus an initial deposit of B₀ dollars grows to

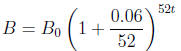
dollars after 52t weeks = t years
.
(iv) The Delaware Bank pays interest compounded daily. This means that
every day it looks at the balance in an account and adds 6/365%. Thus an
initial deposit of B₀ dollars grows to

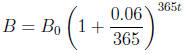
dollars after 365t days = t years.

The general formula for the balance B in a bank account after t years if
the balance is initially B₀, the interest rate is r per year, and the interest is
compounded (i.e. paid) m times per year is

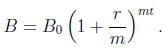
In all cases the formula is of the form

B = B₀a^t

where a = (1 + r/m)^m an the compounding period is 1/m years i.e. the
interest is compounded m times per year, When m becomes infinite we say
that the interest is compounded continuously and in calculus it is proved
that this formula works with a = e^r so the balance after t years is given by

B = B₀e^rt
The following table shows the values of 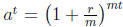for t = 2, r = 0.05,
n = mt, and various values of the number m of compounding periods per
year.

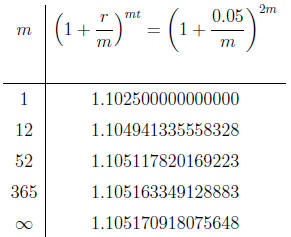
Thus an account with a starting value of $1000 at 5% per year will, in two
years, earn $102.50 in interest if the interest is compounded annually and
$105.17 in interest if the interest is compounded continuously.

Remark 19.4. Presumably in the old days the interest was credited to the
account at the the end of each compounding period and if the account was
closed in the middle of a compounding period the amount of interest earned
since the beginning of the compounding period was forfeited. Today most
banks would use the formula for all values of t not just
when mt is an integer. Of course, the contract signed when the account was
opened will make this precise.

19.5. The doubling time of a quantity N = N₀e^rt which is increasing
exponentially is the time t such that N = 2N₀. Since

2N₀ = N₀e^rt => 2 = e^rt => ln 2 = rt

the doubling time is t = (ln 2)/r. Similarly, the half life of a quantity N =
N₀e^rt which is decreasing exponentially is the time t such that N = N₀/2,
i.e. t = -(ln 2)/r.

20 Complex Numbers

Definition 20.1. The complex numbers are those numbers of form

z = x + iy

where x and y are real numbers and i is a special new number called the
imaginary unit which has the property that i² = -1:The real number x
is called the real part of z and the real number y is called the imaginary
part of z. Two complex numbers are equal iff their real parts are equal and
their imaginary parts are equal. The complex number



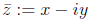
is called the conjugate of z.

20.2. The arithmetic operations are performed by treating i as a variable
and then replacing i² by -1 if necessary. This makes clear that the com-
mutative, associative, and distributive laws hold, that the additive inverse
is 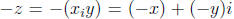so that the law z + (-z) = 0, and that the
rule for multiplying complex numbers is

zw = (x + iy)(u + iv)
= xu + (xv + yu)i + yvi²
= xu + (xv + yu)i - yv
= (xu - yv) + i(xv + yu)

where z = x + iy and w = u + iv and x y, u, v are real. Using the algebraic
law (a + b)(a - b) = a² - b² we see that the product of a complex number
and its conjugate is



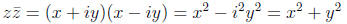
which is a positive real number if z ≠ 0. Hence the multiplication inverse is
defined by



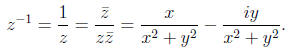
20.3. Conjugation satisfies the following laws.

1. A complex number is real if and only if it is equal to its conjugate:

x + iy = x - iy y = 0 z = x.

2. The conjugate of the conjugate is the original number.



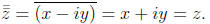
3. Doing an arithmetic operation and then taking the conjugate gives the
same result as taking the conjugates first and then doing the operation:

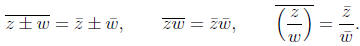
These are all easy to prove. For example if ,
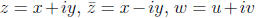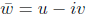then

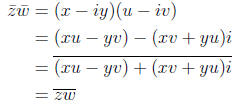
21 Division of Polynomials

Theorem 21.1 (Division Algorithm). Let p(x) and d(x) be polynomi-
als and assume that d(x) is not the zero polynomial. Then the are unique
polynomialsq(x) and r(x) such that

p(x) = d(x) · q(x) + r(x)

and either r(x) is the zero polynomial or the degree of the remainder r(x) is
less than the degree of the divisor d(x).

Proof. Guided Exercise.

Remark 21.2. An analogous statement holds for integers. Let p and d be
be integers with d > 0. Then there are unique integers q and r with

p = d · q + r,
0 ≤ r < d.

For example,

23 = 7 · 3 + 2,
0  ≤ 2 < 7.

In the case of rational numbers (as opposed to rational functions) the condi-
tion that the degree of r(x) is less than the degree of d(x) is replaced by the
condition that the remainder is less than the divisor. In fact there is a very
strong analogy between integers and rational numbers on the one hand and
polynomials and rational functions on the other.

22 The Fundamental Theorem of Algebra

Theorem 22.1 (Fundamental Theorem of Algebra). A polynomial equa-
tion (of positive degree) has a complex root.

Remark 22.2. The proof of the Fundamental Theorem is rather difficult
and is not ordinarily taught in undergraduate courses. The theorem is true
even if the coefficients in the polynomial are complex. In this section we shall
see what the theorem means for real polynomials, i.e. polynomials with
real coefficients.

Theorem 22.3 (Remainder Theorem). If a polynomial f(x) is divided
by (x - r), the remainder is f(r)

Proof. By the Division Algorithm (Theorem 21.1) we have

f(x) = (x - r)q(x) + c (* )

where c is a polynomial of degree less than the degree of the divisor (x - r).
But the degree of the divisor (x - r) is one so the degree of c is zero, i.e. c
is a constant. Now plug in x = r to get f(r) = (r - r)q(r) + c = 0 + c = c
so (* ) becomes f(x) = (x - r)q(x) + f(r).

Corollary 22.4 (Factor Theorem). If r is a root of the polynomial f(x),
then (x - r) evenly divides f(x), i.e. f(x) = (x - r)q(x).

Proof. By the Remainder Theorem just proved we have

f(x) = (x - r)q(x) + f(r).

Hence if f(r) = 0, then f(x) = (x - r)q(x).

Theorem 22.5 (Complete Factorization). Let f(x) be a polynomial of
degree n. Then



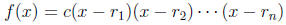
where c is a constant and 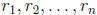are the roots of f(x), i.e. the solutions
of f(x) = 0.

Proof. By the Fundamental Theorem of Algebra, there is a complex number
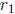such that 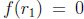so by the Factor Theorem just proved there is a
polynomial 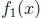such that



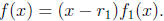
Now 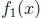is a polynomial of degree n - 1 so by the same argument there is
a complex number 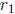and a polynomial of 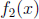with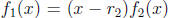
and hence



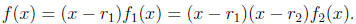
Repeating n times gives



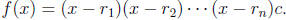
where 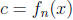has degree 0, i.e. c is constant.

Corollary 22.6. Every real polynomial may be written as a product of real
linear polynomials and real quadratic polynomials with negative discriminant.

Proof. If the coefficients of f(x) are real and r is a complex but non real root
of f(x) then 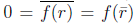so the conjugate 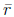is also a root. Let p and
q bet the real and imaginary parts of r so r = p + qi and 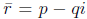. The
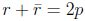and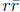 = p² + q². The quadratic polynomial



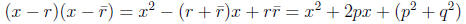
has negative discriminant b² - 4ac = 4p² - 4(p² + q²) = -q². Thus the non
real complex roots occur in pairs in the complete factorization and may be
combined to give the desired factorization into real (quadratic and linear)
polynomials.