Worksheet 11 - Hints and Selected Solution
1. For which sets A is it the case that the only bijection
from A to A is the identity?
Answer. For sets A consisting of exactly one element, as well as for the empty
set.
2. Let A be the set of the days of the week. Let f assign to each day of the
week the number of letters
in its name in English. Is f an injection?
Answer. No. f(Monday) = f(Sunday) but Monday ≠ Sunday.
3. Let A be the set of subsets of 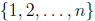 that have
even size, and let B be the set of subsets of
that have
even size, and let B be the set of subsets of
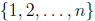 that have odd size. Establish a bijection
from A to B. (
that have odd size. Establish a bijection
from A to B. (![]() )
)
Proof. Let A be the collection of even-sized subsets of
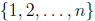 , and let B be the collection of
, and let B be the collection of
odd-sized subsets. For each x ∈ A, define f(x) as follows:
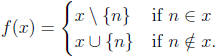
By this definition, #(x) and #(f(x)) differ by one, so f(x)
is a set of odd size and f maps A into
B.
We claim first that f is one-to-one. Consider distinct x, y ∈ A. If both
contain or both omit n,
then f(x) and f(y) agree on whether they contain n but differ outside {n}. If
exactly one of {x, y }
contains n, then exactly one of {f(x), f(y)} contains n. Thus f(x) ≠ f(y), and f
is one-to-one.
We next claim that f is onto. If z ∈ B, then flipping whether n is present
in z yields a subset x
such that f(x) = z, so f is also onto, and hence f is a bijection.
4. Verify that 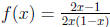 defines a bijection from the
interval [0, 1] to R. (Hint: In the proof that
defines a bijection from the
interval [0, 1] to R. (Hint: In the proof that
f is surjective, use the quadratic formula.) ( )
)
Proof. f is injective Suppose that f(x) = f(y). Then we obtain that
(2x - 1)2y(1 - y) = (2y - 1)2x(1 - x),
which simplifies further to 2(y2 - x2) - 2(y - x) = 4xy(y - x). If y ≠ x, then
we can divide
by 2(y - x) to obtain y + x - 1 = 2xy. Rewriting this as -xy = (x - 1)(y - 1)
makes it clear
that there is no solution when x, y ∈[ 0, 1], since the left side is negative and
the right side is
positive. Therefore we conclude that x = y, and so f is injective.
f is surjective Suppose that f(x) = b. We solve for
x to obtain x ∈[0, 1] such that f(x) = b.
Observe that b = 0 is achieved by 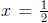 , so we may assume that b ≠ 0. Clearing fractions
, so we may assume that b ≠ 0. Clearing fractions
leads to 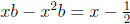 , or
, or
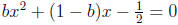 . The quadratic formula yields
. The quadratic formula yields
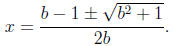
The magnitude of the square root is larger than lbl.
Therefore, choosing the negative sign in
the numerator yields a negative x, which is not in the domain of f. We therefore
choose the
positive sign.
If b > 0, then the square root is less than b + 1, and we obtain
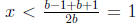 . Also, the
. Also, the
square root is bigger than 1, so x > 0. If b < 0, then let b' = -b. The formula
for x becomes
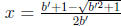 , where b' > 0. the square root is strictly between 1 and
b' + 1, so x is
strictly
, where b' > 0. the square root is strictly between 1 and
b' + 1, so x is
strictly
between 1/2 and 0. In each case, we have found x in the domain [0, 1] such that f(x) = b,
and
we have thus established that f is onto.
5. Let f and g be surjections from R to R, and let h = fg be their product. Must
h also be surjective?
Give a proof or a counterexample.
Counterexample. Let f, g : R → R be defined by f(x) = g(x) = x. Then both f and
g are
surjective, but (f · g)(x) = x2 is not surjective.
6. Determine which formulas below define surjections from
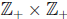 onto
onto 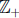 :
:
(a) f(a, b) = a + b.
Answer. Not surjective. (Why?)
(b) f(a, b) = ab.
Answer. Surjective. (Why?)
(c) f(a, b) = ab(b + 1)/2.
Answer. Surjective. (Why?)
(d) f(a, b) = (a + 1)b(b + 1)/2.
Answer. Not surjective. (Why?)
(e) f(a, b) = ab(a + b)/2.
Answer. Not surjective (Why?)
7. Given f : R → R, suppose that there are positive constants c, α such that
for all x, y ∈ R,
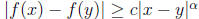 . Prove that f is injective.
. Prove that f is injective.
Proof. Suppose that f is not injective. Then there exist distinct numbers x and
y such that
f(x) = f(y). Since 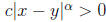 , this contradicts the hypothesis.
, this contradicts the hypothesis.
8. If f : A → B and g : B → C are bijections, prove that
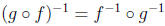 .
.
Proof. We use exercise 11. Since f and g are bijections, both are invertible. Note that
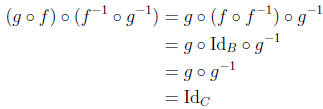
and
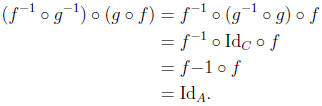
9. Given f : A → B and g : B → C, let h = g o f. Determine
which of the following statements are
true. Give proofs for the true statements and counterexamples for the false
statements.
(a) If h is injective, then f is injective.
Answer. True. (Why?)
(b) If h is injective, then g is injective.
Answer. False. (Why?)
(c) If h is surjective, then f is surjective.
Proof. False. (Why?)
(d) If h is surjective, then g is surjective.
Proof. True. (Why?)
10. Consider f : A → B and g : B → A. Answer each question below by providing a
proof or a
counterexample.
(a) If f(g(y)) = y for all y ∈ B, does it follow that f is a bijection?
Proof. No. (Why?)
(b) If g(f(x)) = x for all x ∈ A, does it follow that f(g(y)) = y for all y ∈ B?
Proof. No. (Why?)
11. Consider f : A → B and g : B → A. Prove that if f o g and g o f are identity
functions, then f is
a bijection. In particular, prove that
(a) If f o g is the identity function on B, then f is surjective.
Proof. If y ∈ B then f(g(y)) = y. Hence there is an element of A mapped to y by
f, namely,
the element g(y). This shows that f satisfies the definition of a surjection.
b) If g o f is the identity function on A, then f is
injective.
Proof. If x ∈ A, we have that g(f(x)) = x. If f is not injective, then there
exist distinct
elements 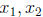 ∈ A such that
∈ A such that
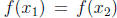 . If we apply g to both sides of the
equality,
. If we apply g to both sides of the
equality,
we obtain 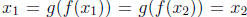 , which contradicts our choice of
distinct elements.
, which contradicts our choice of
distinct elements.
Hence our assumption that f is not injective must be wrong.
12. Consider f : A → A. Prove that if f o f is injective, then f is injective.
Proof. Suppose that f(x) = f(y). Then f(f(x)) = f(f(y)). By the definition of
composition, this
yields (f o f)(x) = (f o f)(y). The hypothesis that f o f is injective yields
now that x = y. We
have proved that f(x) = f(y) implies x = y, and so f is injective.
13. Construct an explicit bijection from the closed interval [0, 1] onto the
open interval [0, 1]. (![]() )
)
Hint. This is a very nice problem. In short, no hint!
14. Consider the function g : R → R defined by
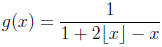
where for any x ∈ R, [x ] denotes the largest natural
number less than or equal to x. (For example,
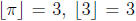 , and
, and 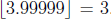 .) Let f : N
→ Q be the function defined by
the following
.) Let f : N
→ Q be the function defined by
the following
rule:
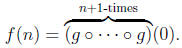
Then prove that f is a bijection between N and
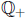 , where
, where 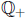 denotes the set
denotes the set
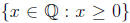 .
.
 (At least convince yourself that this is true!)
(At least convince yourself that this is true!)
Remark. This last exercise should be a final project.


