Inverse Functions
Definition. A function f with domain D and range R is a one-to-one
function if
whenever x1 ≠ x2 in D; then f(x1) ≠ f(x2):
Remark: An equivalent way of writing the condition for a one-to-one
function is
this:
if f(x1) = f(x2); then x1 = x2 in D:
The arrow diagrams ilustrate a function that is one-to-one and a function
that is not
one-to-one.
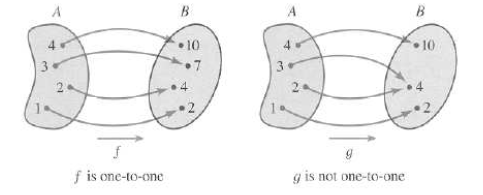
Note that f never takes on the same value twice (any two numbers in A have
different
images), whereas g does take the same value twice (both 2 and 3 have the same
image,
4). In symbols, g(2) = g(3) but f(x1) ≠ f(x2) whenever x1 ≠ x2.
Horizontal line test: A function f is one-to-one if no horizontal line
intersects the
graph of f in more than one point.
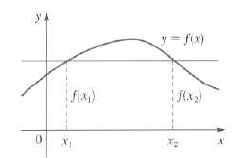
If a horizontal line intersects the graph of f at more than one point (as
shown in the
figure above), then there are numbers x1 ≠ x2 such that f(x1)
≠ f(x2). This
means
that f is not one-to-one.
Remark: The horizontal line test is a geometric method for determining
whether a
function is one-to-one.
Exercises. Determine whether the function is one-to-one:
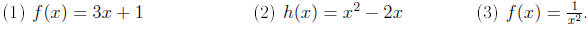
Inverse function.
Definition. Let f be a one-to-one function with domain A and range B. A
function
g with domain B and range A is the inverse of f provided that for every y in B
the
following is true:
g(y) = x if and only if f(x) = y:
The inverse function g is denoted by the symbol f-1. Thus we have
domain of f-1 = range of f
range of f-1 = domain of f
f-1(y) = x if and only if f(x) = y
The definition says that if f takes x into y, then f-1 takes y back into x.
Remark: Don't mistake the -1 in f-1 for an exponent. f-1
does not
mean 1/f(x) .
The reciprocal 1/f(x) is written as (f(x))-1.
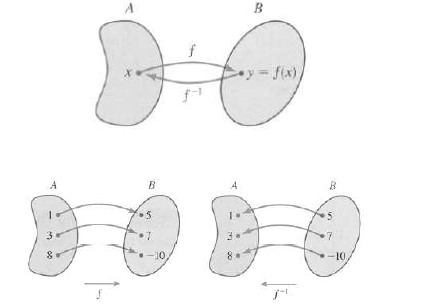
Example: If f(1) = 5, f(3) = 7, and f(8) = -10, find f-1(5), f-1(7),
and f-1(10).
Solution From the definition of f-1, we have: f-1(5) = 1, f-1(7) = 3 and
f-1(10) = 8.
Theorem. Property of Inverse Functions.
Let f be a one-to-one function with domain A and range B. If g is the inverse
function of f then the following conditions are true:
g(f(x)) = x for every x in A
f(g(y)) = y for every y in B:
Conversly, a function g satisfying these equation is an inverse of f.
Using the f-1 notation we have
f-1(f(x)) = x for every x in A
f(f-1(y)) = y for every y in B:
Exercises. Use the Property of Inverse Functions to show that f and g
are inverses
of each other:
(1) f(x) = x + 3 and g(x) = x - 3.
(2) f(x) = x^2 - 4 where x≥0 and g(x) =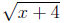
where x≥-4.
(3) f(x) =
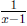where x ≠ 1 and
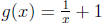where x ≠ 0.
Finding the inverse of a function.
Solve the equation y = f(x) for x in terms of y, obtaining an equation x =
f-1(y).
To write the function f-1 as a function with argument x interchange x and y.
Exercises . Find the inverse of the function f.
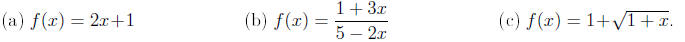
The relationship between the graphs of f and f-1.
First note that b = f(a) is equivalent to a = f-1(b). This implies that the
point
(a; b) is on the graph of f if and only if the point (b; a) is on the graph of
f-1. The
two graphs are re ections of each other through the line y = x, or are symmetric
with
respect to this line.
Example: (a) Sketch the graph of
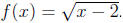(b) Use the graph of f to sketch
the graph of f-1. (c) Find an equation for f-1.
