Math 348 Midterm Test
Instructions: Start each problem 1/2 inch from the top of a new sheet
of
paper. You may, but do not need to work on the back of the sheet. Label
and justify all work. You may work out the answer on scratch paper, but all
scratch paper, along with this sheet, must be handed in.
You may omit one of these four problems for full credit. Cross out here which
problem you are omitting.
Problem 1a Use rules of propositional calculus to show that A
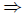 (B
(B 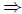 C) is
C) is
equivalent to
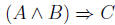 .
.
Problem 1b Use (1a) to formulate the negation of A
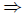 (B
(B 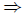 C).
C).
Problem 1c The negation of
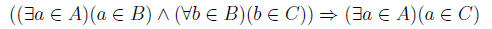
is what in symbols?
Problem 2a Show that 61 is a prime.
Problem 2b Prove that the square-root of a prime is irrational.
Problem 2c Use these two facts plus the quadratic formula to show that the
equation
3x^2 + x − 5 = 0 has no rational solutions.
Problem 3a State the Prime Factorization Theorem accurately and sketch a
proof
using strong induction.
Problem 3b Prove that there are infinitely many prime numbers.
Problem 3c Show that every number not congruent to 0 modulo a prime has a
multiplicative inverse in Zp.
Problem 4a Explain Euclid’s Algorithm (briefly!).
Problem 4b Find all solutions to the Diophantine equation 9x − 3y = 27
Problem 4c Determine (without long division) the
remainders from dividing 43043043
by 2,3,5,7,11 and 13.


